Числовые характеристики распределения данных.

Мы рассмотрели частотное распределение значений рассматриваемого признака. Каждое распределение может дать представление об изучаемой совокупности. Однако, этим анализ распределения данных признака не ограничивается, т.к. частотное распределение ничего не говорит о статистических закономерностях, которые описывали бы числовые характеристики изучаемой совокупности.

К характеристикам распределения, описывающим количественно его структуру и строение относятся :

• характеристики положения;

• рассеивания;

• ассиметрии и эксцесса.

Оценка центральной тенденции

К характеристикам положения относятся следующие оценки центральной тенденции: мода (Мо), медиана (Ме), квантили и среднее арифметическое ( ).

Важное значение имеет такая величина признака, которая встречается чаще всего в изучаемом ряду, в совокупности. Такая величина называется модой (Мо). В дискретном ряду Мо определяется без вычисления как значение признака с наибольшей частотой(например, по данным таблицы 1. Мо= 13).

При расчете моды может возникнуть несколько ситуаций:

1. Два значения признака, стоящие рядом, встречаются одинаково часто. В этом случае мода равна среднему арифметическому этих двух значений. Например, в следующем ряду данных : 12, 13, 14, 14, 14, 16, 16, 16, 18, 19

Мо= (14+16)/2= 15.

2. Два значения, встречаются также одинаково часто, но не стоят рядом. В этом случае говорят, что ряд данных имеет две моды, т.е. он бимодальный.

3. Если все значения данных встречаются одинаково часто, то говорят что ряд не имеет моды.

Чаще всего встречаются ряды данных с одним модальным значением признака. Если в ряду данных встречается два или более равных значений признака, то говорят о неоднородности совокупности.

Вторая числовая характеристика ряда данных называется медианой (Ме) – это такое значение признака, которое делит ряд пополам. Иначе, медиана обладает тем свойством, что половина всех выборочных значений признака меньше её, половина больше. При нечетном числе элементов в ряду данных, медиана равна центральному члену ряда, а при четном среднему арифметическому двух центральных значений ряда. В нашем примере (таблица 1.) Ме=(13+13)/2=13. Вычисление медианы имеет смысл только для порядкового признака.

Среднее арифметическое значение признака

М = ,

где x_i – значения признака, n – количество данных в рассматриваемом ряду.

Среднее арифметическое значение признака, вычисленное для какой-либо группы, интерпретируется как значение наиболее типичного для этой группы человека. Однако бывают случаи, когда подобная интерпретация несостоятельна (в случае, если существует большая разница между минимальным и максимальным значениями признака).

Квантиль – это такое значение признака, которое делит распределение в заданной пропорции: слева 0,5%, справа 99,5%; слева 2,5%, справа 97,5% и т.п. Обычно выделяют следующие разновидности квантилей:

Квартили Q₁, Q₂, Q₃ – они делят распределение на четыре части по 25% в каждой;

Квинтили К₁, К₂, К₃, К₄ – они делят распределение на пять частей по 20% в каждой;

Децили D₁, ..., D₉, их девять, и они делят распределение на десять частей по 10% в каждой;

Процентили P₁, Р₂ ...,Р₉₉, их девяносто девять, и они делят распределение на сто частей по 1% в каждой части.

Поскольку процентиль - наиболее мелкое деление, то все другие квантили могут быть представлены через процентили. Так, первый квартиль - это двадцать пятый процентиль, первый квинтиль - второй дециль или двадцатый процентиль, и т.п.

Характеристики рассеивания

Используя для описания ряда значений признака, только меру центральной тенденции, можно сильно ошибиться в оценке характера изучаемой совокупности. Это хорошо видно на следующем примере. Допустим, мы изучаем средний возраст в двух группах, состоящих каждая из 6-ти человек.

Значения признака распределились следующим образом:

1 группа – 10, 10, 10, 50, 50, 50

2 группа – 30, 30, 30, 30, 30, 30

Подсчитав среднее значение в каждой из групп, получим 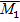= 30 и 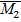=30. Т.е. мы получили одинаковые значения, тогда как совершенно очевидно, что выборки взяты из разных совокупностей.

Ошибка произошла из-за разброса значений возраста в этих группах.

Существует несколько способов оценки степени разброса или рассеивания данных. Основными характеристиками рассеивания являются: размах (R), дисперсия (D), среднеквадратическое (стандартное) отклонение (σ - сигма), коэффициент вариации( V).

Простейший из параметров распределения, размах - это разность между максимальным и минимальным значениями признака: R = x_max - x_min .

Дисперсия показывает разброс значений признака относительно своего среднего арифметического значения, то есть насколько плотно значения признака группируются вокруг ; чем больше разброс, тем сильнее варьируются результаты испытуемых в данной группе, тем больше индивидуальные различия между испытуемыми:

.

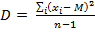Из формулы видно, что дисперсия имеет "квадратный размер": если величина измерена в баллах, то дисперсия характеризует ее разброс в "баллах в квадрате", и т.п. Большую наглядность в отношении разброса имеет среднеквадратическое отклонение, так как его размерность соответствует размерности измеряемой величины:

.

Коэффициент вариации вообще не имеет размерности, что позволяет сравнивать вариативность случайных величин, имеющих различную природу:

* 100%.