Метод дисконтирования денежных потоков

Применение данного метода наиболее обосновано для оценки предприятий, денежные потоки которых нестабильны.

Метод дисконтирования денежных потоков – определение стоимости имущества суммированием текущих стоимостей ожидаемых от него потоков дохода.

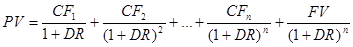
PV-текущая стоимость; CF_n- доход n-го периода; FV-реверсия (расчет величины стоимости имущества (предприятия) в постпрогнозный период); DR – ставка дисконтирования; n – последний год прогнозного периода.

В вышеприведенной формуле денежные потоки дисконтируются, как если бы они были получены в конце года. Иногда оценщик считает целесообразным дисконтировать денежные потоки, как если бы предполагалось их получение в середине прогнозного года (в частности, при сезонности производства, или с учетом того, что доход поступает частями в течение года, а не единовременно общей суммой в конце года). Тогда формула принимает вид:

81. Учёт стоимости денег во времени при оценке имущ-ва доходным подходом.

Для анализа разновременных денежных потоков, обоснова­ния инвестиционных вложений, определения стоимости недви­жимости и бизнеса, а также выполнения ряда других операций применяют элементы финансовой математики.

При расчете нормы дохода на инвестируемый капитал долж­на учитываться текущая стоимость будущих доходов для сопо­ставимости с текущей стоимостью инвестиций, иначе будущие доходы в случае их преобразования в текущую стоимость могут оказаться равными капитальным вложениям.

При вложении средств инвестор отказывается от текущего по­требления в надежде получить больший доход в будущем, одна­ко существует риск неполучения ожидаемого дохода. Поэтому инвестор заслуживает премии, что является ключевым фактором необходимости учета стоимости денег во времени.

Основные причины изменения стоимости денег во времени:

1) инвестор отказывается от текущего потребления, за что за­служивает премии;

2) инвестор берет на себя риск неполучения ожидаемого до­хода, что требует учета премии за риск, связанный с объектом инвестирования;

3) меняется покупательная способность денег.

Для анализа денежных потоков от недвижимости и бизнеса, для определения текущей стоимости инвестиций, обоснования величины платы за получение будущих потоков дохода, широко применяются функции сложных процентов. Что это такое?

Простой процент — процент, начисляемый только на основ­ную сумму долга без учета накопленных процентов.

Сложный процент — процент, начисляемый на основную сум­му долга и невыплаченные ранее проценты, начисленные за пре­дыдущий период.Основные области применения сложного процента:

1) будущая стоимость единицы;

2) накопление единицы за период;

3) фактор фонда возмещения;

4) текущая стоимость единицы;

5) текущая стоимость единичного аннуитета*;

6) взнос за амортизацию денежной единицы.

Для удобства в работе с различными потоками доходов исполь­зуют финансовые калькуляторы. Они имеют клавиши числа пе­риодов, периодической ставки процента, периодического плате­жа, текущей стоимости суммы, будущей стоимости суммы и др. Для упрощения расчетов в случае отсутствия финансового каль­кулятора применяют таблицы сложных процентов.

Функции сложного процента. Будущая стоимость единицы (Sⁿ) — будущая стоимость од­ной денежной единицы через п периодов при ставке сложного процента i. Sⁿ=(1+i)ⁿ

где Sⁿ — сумма после и периодов;

i — периодическая фактическая ставка процента; п — число периодов.

Пример . Необходимо определить будущую стоимость 1 000 000 руб. при ставке сложного процента 30%, если период накопления соста­вит пять лет:

1 000 000 х (1 + 0,3)⁵ = 3 712 930 (руб.). Используем для решения этой задачи таблицы сложных процентов. Инвестор, зная стоимость одного рубля к концу пятого года накопле­ния, может узнать будущую стоимость одного миллиона рублей, умно­жив будущую стоимость одного рубля на вложенную сумму: 1 000 000 х 3,71293 = 3 712 930 (руб.).

Накопление единицы за период (S_n) — остаток денежных средств через и периодов при ставке сложного процента, равной i, в результате периодического пополнения основной суммы де­позита за счет новых взносов и перевода накопленных процен­тов в основную сумму депозита:

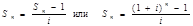
Таким образом, при вкладе на три года рубль, депонирован­ный в конце первого года, будет приносить процент в течение двух лет; рубль, депонированный в конце второго года, — в тече­ние одного года; рубль, депонированный в конце третьего года, не принесет процента.

Фактор фонда возмещения (SFF) показывает денежную сумму, которую необходимо депонировать в конце каждого периода для того, чтобы через п периодов при ставке сложного процента, равной i_t остаток на счете составил один рубль:

Периодический платеж = Желаемая сумма х SFF.

Пример . Если остаток на депозите приносит ежегодно 20% дохо­да, то для того, чтобы за три года накопить 3,64 млн руб., нужно ежегод­но вкладывать по 1 млн руб.:

0,27473 х 3,64 = 1 (млн руб.)

Коэффициент текущей стоимости единицы (фактор дисконти­рования, DF) — это текущая стоимость одной денежной едини­цы, которая должна быть получена через п периодов при ставке сложного процента, равной /:

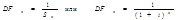
Пример . При ставке дисконтирования 20% текущая стоимость 1 млн руб., ожидаемого к получению через год, составит 833 тыс. руб.:

DF_t=\: (1+0,20)' = 0,833; 0,833 х 1 млн руб. = 833 тыс. руб.

Текущая стоимость единичного аннуитета (а_я) —текущая стоимость серии ожидаемых равных единичных поступлений в течение п периодов при ставке сложного процента, равной

Пример . Право получения 100 тыс. руб. дохода в конце каждого года в течение следующих трех лет можно оценить следующим образом:

a_t = 2,106 тыс. руб. 100 х 2,106 = 210,6 (тыс. руб.).

Следовательно, текущая стоимость инвестиций 210,6 тыс. руб. яв­ляется обоснованной платой за право получения 100 тыс. руб. в конце каждого следующего года в течение трех лет при ставке 20%.

Взнос на амортизацию денежной единицы— коэффициент ча­стичных платежей, который показывает величину обязательно­го периодического платежа, необходимую для погашения кре­дита за п периодов при ставке сложного процента, равной

Амортизация денежной единицы — это процесс погашения долга в течение определенного времени. Взнос на амортизацию кредита математически определяется как отношение одного пла­тежа к первоначальной сумме кредита.

Функции сложного процента взаимосвязаны и применяются в оценке имущества с использованием доходного подхода.