ОСНОВНЫЕ ПОНЯТИЯ И КЛАССИФИКАЦИЯ ВИДОВ ИГР

Игра – это упрощенная формализованная модель реальной конфликтной ситуации. Формализация означает выработку определенных правил действия сторон в процессе игры: варианты действия сторон, исход игры при данном варианте, степень информированности каждой стороны о поведении всех других сторон.

Заинтересованные играющие стороны (в частности, лица) называются игроками. Причем одну играющую сторону может представлять как один игрок, так и целый коллектив.

Стратегией игрока называется любое возможное для игрока действие в рамках заданных правил игры. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемых ситуацией.

Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней. Хотя не каждый выигрыш можно оценить количественно, но в теории игр качественные выигрыши не рассматриваются.

Классифицировать игры можно по следующим критериям:

1. Количество игроков. Если в игре участвуют две стороны, то ее называют игрой двух лиц. Если число сторон больше двух, ее называют игрой n лиц (или множественной). Наиболее глубоко проработаны игры двух лиц.

2. Количество стратегий игры. По этому критерию игры делятся на конечные и бесконечные. В конечной игре каждый из игроков имеет конечное число возможных стратегий. Игра является бесконечной, если хотя бы один из игроков имеет бесконечное число возможных стратегий.

3. Взаимоотношения сторон. По этому критерию игры подразделяются на бескоалиционные, коалиционные, кооперативные. Бескоалиционной называется игра, в которой игроки не имеют права вступать в соглашения, образовывать коалиции. В коалиционной игре игроки могут вступать в соглашения, образовывать коалиции. Если коалиции определены заранее, то такая игра называется кооперативной.

4. Характер выигрышей. По этому критерию игры подразделяются на игры с нулевой суммой и игры с ненулевой суммой. Игра с нулевой суммой означает, что сумма выигрышей всех игроков в каждой партии равна нулю. Игры двух игроков с нулевой суммой относятся к классу антагонистических игр. При этом выигрыш одного игрока равен, естественно, проигрышу другого игрока. Игра, в которой нужно вносить взнос за право участия в ней, является игрой с ненулевой суммой. Экономические задачи теории игр относятся к обоим типам игр.

5. Вид функций выигрыша. По этому критерию игры подразделяются на матричные, биматричные, непрерывные, выпуклые, сепарабельные и так далее.

Матричная игра - конечная игра двух игроков с нулевой суммой. Предположим, что первый игрок имеет 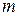стратегий 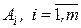, а второй игрок 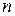стратегий 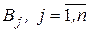. Тогда игра может быть названа игрой 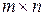(эм на эн) или 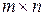игрой. Обозначим через 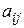значения выигрышей игрока (соответственно - значения проигрышей игрока ), если первый игрок выбрал стратегию 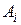, а второй игрок стратегию . В этом случае говорят, что имеет место ситуация 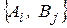. Значения выигрышей 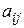(эффективностей) можем представить в виде платежной таблицы, называемой матрицей игры или платежной матрицей:

Таблица 1.1

	Игрок 2
		…
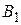
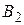
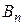
Игрок 1				…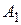
			…
…	…	…	…	…
			…

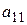
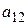
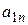
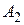
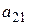
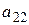
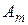
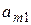
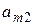
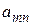
Или в виде матрицы:

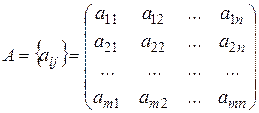. (1.1)

Биматричная игра - конечная игра двух игроков с ненулевой суммой. Выигрыш каждого игрока задается своей платежной матрицей вида (1).

Если функция выигрышей

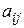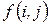= (1.2)

является непрерывной, то игра называется непрерывной, если (2) выпуклая, то игра называется выпуклой; если (2) можно представить в виде суммы произведений функций одного аргумента - сепарабельной.

6. Количество ходов. По этому критерию игры делятся на одношаговые или многошаговые. Одношаговые заканчиваются после одного хода каждого игрока, и происходит распределение выигрышей. Многошаговые игры бывают позиционными, стохастическими, дифференциальными и так далее.

7. Информированность сторон. По этому критерию различают игры с полной и неполной информацией. Игра определяется как игра с полнойинформацией, если каждый игрок на каждом ходу игры знает все стратегии, примененные ранее другими игроками на предыдущих ходах. Если же игроку известны не все стратегии предыдущих ходов других игроков, то игра называется игрой с неполной информацией.

8. Степень неполноты информации. По этому критерию игры делятся на статистические и стратегические. Стратегические игры проходят в условиях полной неопределенности. Статистические игры проводятся в условиях частичной неопределенности. В статистической игре имеется возможность получения информации на основе статистического эксперимента, по результатам которого оценивается распределение вероятностей стратегий игроков. И с теорией статистических игр тесно связана теория принятия экономических решений.

Изучение теории игр можно проводить с различных точек зрения. Мы будем стремиться решать следующие задачи:

1. Выработка принципов оптимальности, то есть того, какое поведение игроков следует считать разумным или целесообразным.

2. Выяснение реализуемости принципов оптимальности, то есть установление существования оптимальных ситуаций (и стратегий).

3. Отыскание оптимальных ситуаций (реализация игры).

Отметим также, что оценка игроком ситуации путем указания его количественного выигрыша, вообще говоря, возможна не всегда, а иногда просто не имеет смысла. В этом случае численное значение выигрыша в каждой ситуации заменяют на сравнительную предпочтительность ситуаций для отдельных игроков. Тогда речь ведут о теории игр с предпочтениями, которая включает в себя теорию игр с выигрышами как частный случай.

Таким образом, основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявления для каждого из них «оптимальной стратегии». Понятие оптимальной стратегии - одно из важнейших понятий теории игр, и может пониматься в различных смыслах в зависимости от показателя оптимальности (эффективности). Стратегия, оптимальная по одному показателю может не быть оптимальной по другому. Поэтому чаще всего оптимальная стратегия, определенная в результате применения теории игр к реальным конфликтным ситуациям является оптимальной теоретически и в большинстве случаев, реально удовлетворительной.

ГЛАВА II.

МАТРИЧНЫЕ ИГРЫ