КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РЕШЕНИЕ МАТРИЧНОЙ ИГРЫ 2×2
Начнем рассмотрение методов нахождения оптимальных смешанных стратегий с простейшей игры, описываемой платежной матрицей
 .
.
Пусть смешанные стратегии игроков имеют вид:
 ,
,  .
.
Оптимальные стратегии  и
и 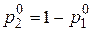 , и цена игры
, и цена игры 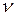 должны удовлетворять условиям:
должны удовлетворять условиям:
 (2.14)
(2.14)
или
 .
.
Откуда получаем следующее решение матричной игры:
 (2.15)
(2.15)
Вычислив оптимальное значение 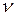 , можем вычислить и оптимальную смешанную стратегию второго игрока из условия
, можем вычислить и оптимальную смешанную стратегию второго игрока из условия 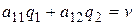 , или
, или 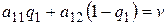 . А именно:
. А именно:
 , (2.15')
, (2.15')
при  .
.
Эту задачу можно решить и графически, учитывая, что решение системы (2.14) представляет собой геометрически точку пересечения двух прямых на плоскости 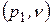 или
или 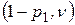 .
.
Приведем алгоритм геометрического способа решения игры 2×2:
1. На оси абсцисс откладываем отрезок единичной длины 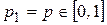 .
.
2. На оси ординат откладываем выигрышы при стратегии 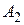 , а на прямой
, а на прямой 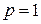 - выигрыши при стратегии
- выигрыши при стратегии 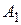 .
.
3. Строим стратегии, проходящие через точки:
а)  и
и 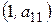 ;
;
б) 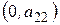 и
и 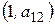 .
.
4. Находим точку пересечения прямых, которая и дает решение матричной игры  .
.
Проиллюстрируем данный алгоритм на рисунке:
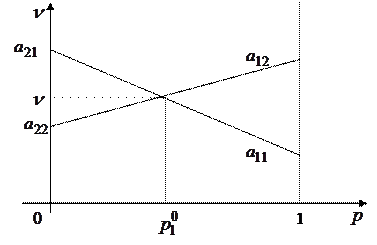 |
Рис. 2.1
№ 2.5.Решите матричную игру  , заданную платежной матрицей:
, заданную платежной матрицей:
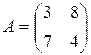 .
.
Решение. Определим сначала верхнюю и нижнюю цену игры:
 ,
,
 .
.
Так как  , то имеем игру без седловой точки, что приводит к необходимости рассмотрения смешанной стратегии. По формулам (2.15) найдем:
, то имеем игру без седловой точки, что приводит к необходимости рассмотрения смешанной стратегии. По формулам (2.15) найдем:
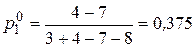 ,
,
 ,
,
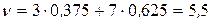 .
.
По формулам (2.15´) определим смешанную стратегию второго игрока:
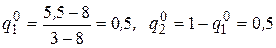 .
.
Ответ:  .
.
Проиллюстрируем это решение графически согласно приведенному выше алгоритму.
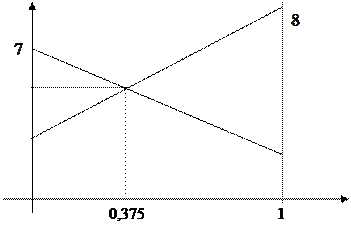 |
|
|
|
|
|
|
Рис.2.2
Дата добавления: 2015-01-29; просмотров: 305; Мы поможем в написании вашей работы!; Нарушение авторских прав |