Итерационный метод решения матричных игр

Этот метод решения матричной игры отражает, в некоторой степени, реальную ситуацию накопления опыта по поиску игроками хороших стратегий в результате многократного повторения конфликтных ситуаций. На каждом шаге игрок выбирает наиболее выгодную для себя стратегию, опираясь на предыдущий выбор противника. То есть игрок на собственном опыте прощупывает способ поведения другого игрока и старается отвечать на него наиболее выгодным для себя образом.

Таким образом, происходит практическое «обучение» игроков в ходе самой игры. Проиллюстрируем итерационный метод на следующем примере.

№ 2.8.Найти итерационным методом решение матричной игры :

.

Решение. Вычислим , то есть седловой точки нет, и необходимо строить смешанную стратегию.

Найдем сначала точное решение геометрическим способом:

.

Теперь опишем правила выбора ходов (чистых стратегий) игроками, предположив для определености, что начинает первый игрок. Пусть первый игрок выберет стратегию :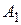

.

Второй игрок ответит стратегией , чтобы выигрыш первого игрока был минимален:

.

В ответ первый игрок выберет стратегию 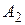, чтобы его выигрыш был максимальным:

.

Второй игрок выбирает свою стратегию так, чтобы “накопленный” выигрыш первого игрока

,

был минимален - это стратегия .

Первый игрок выбирает свою стратегию так, чтобы его «накопленный» выигрыш при стратегиях и был максимален:

,

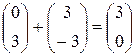это стратегия .

Второй игрок выбирает свою стратегию снова из условия минимума «накопленного» выигрыша первого игрока:

,

например, эта стратегия и так далее.

Разобьем последовательные ходы игроков на пары и запишем результаты в таблице:

Таблица 2.4

n	i					j
					0,00					1,50
					0,00				1,5	0,75
					1,00				1,0	1,0
					0,75				1,5	1,125
					0,6				1,2	0,9
					1,0				1,0	1,0
					0,857				1,286	1,071
					0,75				1,125	0,9375
					1,0				1,0	1,0
					0,9				1,2	1,05
					0,818				1,091	0,955
					1,0				1,00	1,00

Дадим пояснения по составлению таблицы:

1 - ый столбец – номер пары ходов игроков.

2 -ой столбец – номер стратегии 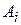, выбранной первым игроком.

3 - ий, 4 – ый и 5 - ый столбцы – «накопленный» суммарный выигрыш первого игрока за первые n шагов, при выборе вторым игроком стратегий 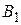, и соответственно. Минимальный из этих выигрышей выделен жирным шрифтом и служит основанием для ответного хода второго игрока.

6 - ой столбец – минимальный средний выигрыш первого игрока за первые n ходов.

7 - ой столбец – номерстратегии , выбранной вторым игроком.

8 – ой и 9 - ый столбцы – «накопленный» суммарный выигрыш первого игрока за первые n шагов при выборе им стратеги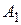й и 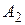соответственно. Максимальный выигрыш выделен жирным шрифтом и служит основанием для нового хода первым игроком.

10 - ый столбец – максимальный средний выигрыш первого игрока за первые n ходов.

11 - ый столбец – среднее арифметическое минимального и максимального среднего выигрышей первого игрока.

Считая, что смешанные стратегии игроков оцениваются частотами появлений чистых стратегий, можем на каждом шаге найти приближенно эти стратегии:

Таблица 2.5

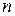
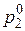
						1,5
	1/2	1/2		1/2	1/2	0,75
	2/3	1/3		2/3	1/3	1,0
	3/4	1/4		3/4	1/4	1,125
---	---	---	---	---	---	---
	5/8	3/8		5/8	3/8	0,9375
---	---	---	---	---	---	---
	7/11	4/11		7/11	4/11	0,955
	2/3	1/3		2/3	1/3	1,00
-	-	-	-	-	-	-

Видно, что с увеличением числа шагов приближенные значения вероятностей все меньше отличаются от точных значений.

Отметим два основных преимущества данного метода:

1) Метод прост и универсален.

2) Объем и сложность вычислений сравнительно слабо растут при увеличении числа стратегий и 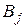игроков.