СМЕШАННЫЕ СТРАТЕГИИ.

Рассмотрим теперь подробнее случай отсутствия седловой точки, то есть случай, когда . Это означает, что первый игрок может обеспечить себе выигрыш, не меньший , а второй проигрыш не больший . Возникает вопрос, как «справедливо» разделить разность 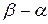между игроками.

Оказывается, что компромиссного распределения разности 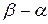между игроками можно добиться путем случайного чередования игроками чистых стратегий. При этом можно получить выигрыш «в среднем» больший, чем , но меньший, чем .

Для этого применяют так называемые смешанные стратегии, которые можно представить в виде случайных величин, возможными значениями которых являются чистые стратегии.

Для первого игрока имеем смешанную стратегию

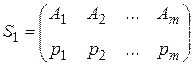, (2.7)

где , - вероятность того, что первый игрок применит чистую стратегию , .

А для второго игрока имеем смешанную стратегию:

, (2.7’)

где , - вероятность того, что второй игрок применит чистую стратегию , .

Отметим, что каждая чистая стратегия является частным случаем смешанной стратегии.

Если мы окажемся в ситуации 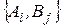, то она будет реализована с вероятностью , а выигрыш составит величину 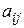. И средний выигрыш первого игрока можно определить как математическое ожидание:

, (2.8)

где - вектора с компонентами и соответственно.

Стратегии и называются оптимальными смешанными стратегиями игроков, если выполнены следующие соотношения:

. (2.9)

Поясним последнее соотношение. Левая часть этого неравенства означает, что если первый игрок отклоняется от оптимальной стратегии , то его выигрыш может только уменьшиться, при условии, что второй игрок придерживается оптимальной стратегии . Аналогично неравенство: означает, что если второй игрок отклоняется от оптимальной стратегии , то его проигрыш может только увеличиться.

Условие оптимальности (2.9) аналогично условию

. (2.10)

И величина

(2.11)

будет называться ценой игры, а набор называется решением матричной игры.

Естественно, что возникают следующие вопросы: какие матричные игры имеют решение в смешанных стратегиях и как найти это решение, если оно существует. Ответ на этот вопрос дает основная теорема теории матричных игр.

Теорема 2.1. (Неймана). Для матричной игры с любой матрицей величины

,

существуют и равны между собой:

= .

Более того, существует, по крайней мере, одна ситуация 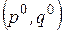, для которой выполняется соотношение:

= = . (2.12)

Другими словами, любая матричная игра имеет решение в смешанных стратегиях.

В состав оптимальных смешанных стратегий игроков могут входить не все чистые стратегии , то есть вероятности некоторых из них будут равны нулю 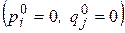. Тогда те чистые стратегии , которые входят в оптимальные смешанные стратегии, будут называться активными чистыми стратегиями. На этот счет справедлива следующая теорема:

Теорема 2.2. Оптимальная смешанная стратегия первого игрока смешивается только из тех чистых стратегий 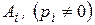, для которых выполнены равенства

;

А в оптимальной смешанной стратегии второго игрока смешиваются только те стратегии 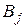, для которых выполнены равенства

.

Кроме того, справедливы равенства:

. (2.13)

Последние равенства и представляют собой основу для разработки различных методов решения матричных игр.

Таким образом, можно привести следующие условия применения смешанных стратегий:

1. Игра без седловой точки.

2. Игроки используют случайную смесь чистых стратегий с заданными вероятностями.

3. Игра повторяется многократно в сходных условиях.

4. При любом ходе ни один из игроков не информирован о стратегии второго игрока.

5. Допускается усреднение результатов игр.

Перейдем теперь к изучению методов решения матричных игр в смешанных стратегиях.