ПРИМЕРЫ МАТРИЧНЫХ ИГР

Для того, чтобы составить экономико-математическую модель конфликтной ситуации в виде матричной игры, необходимо построить матрицу выигрышей. Это весьма нетривиальная задача, особенно для игр большой размерности. В общем виде матрица игры (платежная матрица) строиться следующим образом:

1) перечисляем все возможные чистые стратегии и игроков;

2) формализуем правила, по которым развивается конфликт в виде функции выигрышей .

Рассмотрим несколько примеров построения платежных матриц.

№ 2.1. (Поставка товаров). На каждой из двух баз ассортиментный минимум составляет один и тот же набор из 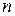видов товаров. Каждая база должна поставить в свой магазин только один из этих видов товара. Магазины, обозначим их через и конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в магазин , более высокого качества. Если магазин завезет с базы товар -ого вида ( ), а магазин -товар -ого вида ( ), отличной от товара -ого вида ( ), то товар -ого вида будет пользоваться спросом и магазин получит прибыль у.е. Если же в магазины и завезены товары одинакового вида ( ), то товар -ого вида в магазине не будет пользоваться спрос м, так как такой же товар, но более высокого качества продается в магазине ,по такой же цене. Поэтом у магазин понесет убытки по транспортировке, хранению и возможно порче товара -ого вида в размере у.е.

Требуется составить платежную матрицу игры при .

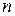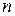Решение. Формализуем данную конфликтную ситуацию. Пусть в качестве первого игрока выступает магазин , и в качестве 2-го – магазин . Игрок с целью достижения прибыли имеет возможность выбрать одну из следующих стратегий - завезти ее со своей базы товар -ого вида. Игрок также обладает стратегиями - завезти ее со своей базы - ый товар. Пусть игроки выбрали стратегии . Тогда можно составить следующую функцию выигрышей игрока :

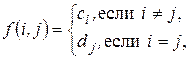
а платежная матрица (матрица игры), например, при будет выглядеть следующим образом:

.

№ 2.2.(антагонистическая конкуренция). Фирма производит некоторый сезонный товар, имеющий спрос в течение 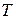единиц времени, и который она может поставить на рынок в один из моментов времени . Для конкурентной борьбы с фирмой дочерняя фирма концерна , не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в один из моментов времени . Пусть технология выпуска товара такова, что чем дольше он находится в производстве, тем выше его качество, а реализуется только товар более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени равен у.е.

Требуется построить функцию выигрышей фирмы , где под выигрышем понимается доход фирмы . при этом единственным законным средством фирмы в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены, на поставляемый товар, запрещено определенными соглашениями.

Решение. Формализуем данную конфликтную ситуацию. В качестве игроков выступают фирмы и , которые преследуют прямо противоположные интересы: фирма стремится максимизировать свой доход, а фирма - минимизировать его. Для достижения своей цели фирма обладает 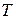стратегиями: , где , ( )- стратегия, состоящая в том, что фирма поставляет товар на рынок в момент времени . Фирма обладает аналогичными стратегиями . Рассмотрим три возможных варианта результатов сравнения моментов поставки товаров фирмами и .

1) Если 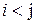, то в течение ( ) ед. времени фирма не будет иметь конкурента и ее доход составит величину у.е. В момент времени на рынке появляется товар фирмы , который имеет более высокое качество, так как он поступает на рынок позже. Поэтому, начиная с момента времени фирма теряет рынок и дохода в дальнейшем не получает.

2) Если , то обе фирмы поставляют свой товар на рынок одновременно, поэтому фирма (так же как и фирма ) в оставшиеся ед.времени получит ровно половину дохода в размере у.е.

3) Если 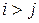, то товар фирмы более качественный, поэтому в течение оставшихся ед.времени, фирма получит доход в размере у.е.

Таким образом, функция выигрышей игрока может быть записана в виде:

Если предположить, например, что , то можно составить следующую платежную матрицу игры:

.