МАТРИЧНЫЕ ИГРЫ 2×n.

Пусть платежная матрица игры имеет вид:

.

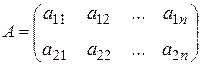Тогда, согласно теореме 2.2, решение игры находится из уравнения:

.

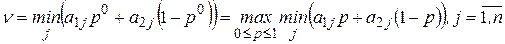Для нахождения максимума (по 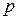) функции

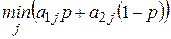, (2.16)

построим ее график. Для этого надо построить n прямых вида:

, (2.16´)

на плоскости 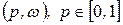и путем визуального сравнения выбрать ломанную, огибающую их снизу. Верхняя точка этой ломанной и дает решение игры.

Геометрически это можно проиллюстрировать следующим образом:

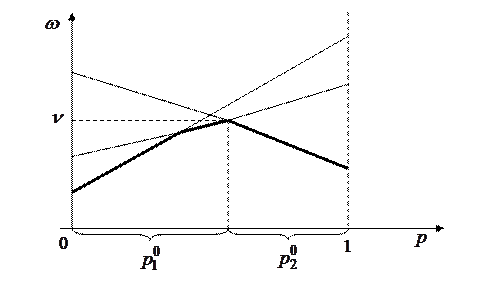
Рис.2.3

Здесь функция (16) выделена жирной линией.

№ 2.6.Найти оптимальную стратегию первого игрока в матричной игре, заданной матрицей 2×3:

.

Решение. 1. Сначала проанализируем игру на наличие седловой точки:

,

.

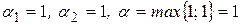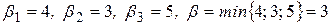Так как , то седловой точки нет и надо искать решение в смешанных стратегиях.

2. Вычислим средние выигрыши первого игрока, при условии, что второй игрок выбирает только чистые стратегии, при помощи таблицы:

То есть, получаем следующие прямые:

,

,

.

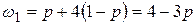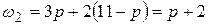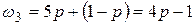3. Построим нижнюю огибающую данных трех прямых:

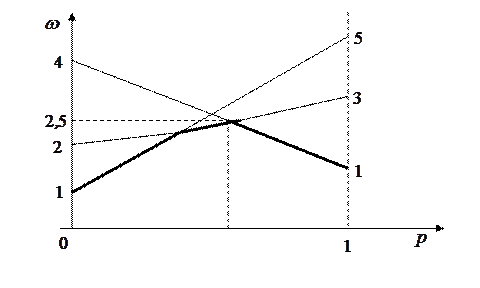
Рис.2.4

4. Видно, что максимальное значение огибающей определяется точкой пересечения прямой с прямой 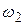. Поэтому решаем систему уравнений:

а именно,

.

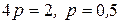Следовательно, получили следующее решение:

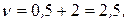
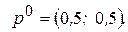
Найдем теперь оптимальную стратегию для второго игрока. Здесь в зависимости от формы нижней огибающей может представиться несколько случаев.

А) Нижняя огибающая имеет единственную точку максимума ( ).

1. Если 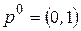, то есть оптимальной стратегией первого игрока является стратегия 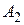, то второму игроку выгодно применять чистую стратегию, соответствующую номеру прямой ( ), проходящей через точку ( ) и имеющий наибольший отрицательный наклон.

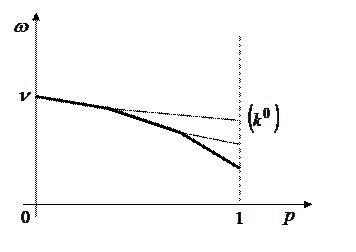
Рис.2.5

3. Если 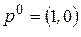, то оптимальной для второго игрока является стратегия, соответствующая номеру ( ) соответствующей прямой, имеющей наименьший положительный наклон.

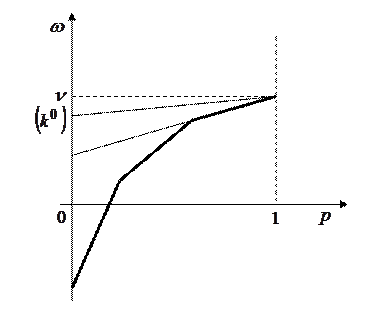
Рис.2.6

4. Если 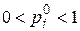, то в оптимальной точке пересекаются как минимум две прямые:

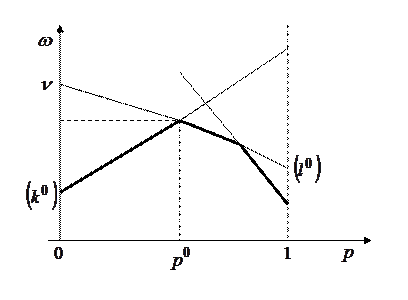
Рис.2.7

одна из которых ( ) имеет положительный наклон, а другая ( ) отрицательный. И оптимальная смешанная стратегия второго игрока получается при

где является решением уравнения

.

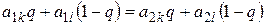B) Нижняя огибающая имеет горизонтальный участок.

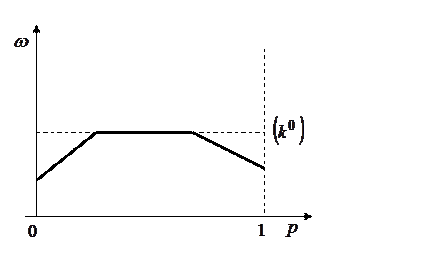
Рис.2.8

Тогда оптимальной для второго игрока является чистая стратегия .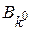

Найдем теперь оптимальную стратегию второго игрока в нашей задаче.

1) Так как в оптимальной точке пересекаются первые две прямые, то

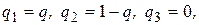
то есть из трех стратегий применяются первые две (активными являются 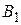и ).

2) Приравняем соответствующие средние выигрыши второго игрока с использованием таблицы:

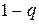
а именно,

.

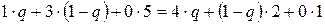3) Решим последнее уравнение:

,

.

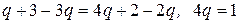4) Вычислим цену игры:

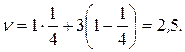
Следовательно, полное решение игры имеет вид: