
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доминирование стратегий
В ряде случаев анализ платежной матрицы показывает, что некоторые чистые стратегии не могут внести никакого вклада в оптимальные смешанные стратегии, поэтому их можно отбросить, что приводит к платежной матрице меньшей размерности.
Пусть 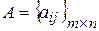 - произвольная платежная матрица.
- произвольная платежная матрица.
Говорят, что стратегия 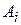 доминирует стратегию
доминирует стратегию  , если справедливы неравенства:
, если справедливы неравенства:
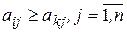 .
.
В этом случае из платежной матрицы можно «убрать»  - ую строку.
- ую строку.
Аналогично, стратегия 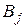 доминирует стратегию
доминирует стратегию 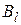 , если
, если
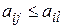 ,
, 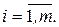
В этом случае из матрицы можно «убрать» 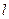 - ый столбец.
- ый столбец.
Рассмотрим применение доминирования стратегий на примере следующей матрицы выигрышей:
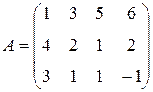 .
.
Очевидно, что все элементы второй строки (стратегия 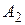 ) не меньше соответствующих элементов третьей строки, поэтому третью строку можно удалить. Тогда получим матрицу
) не меньше соответствующих элементов третьей строки, поэтому третью строку можно удалить. Тогда получим матрицу  :
:
 .
.
Сравнивая поэлементно третий и четвертый столбцы, видим, что третий столбец доминирует четвертый, поэтому его также можно удалить:
 ,
,
а решение последней задачи можно найти (№ 2.7), например, графическим способом:
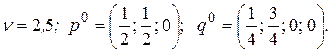
Мажорирование стратегий можно распространить и на смешанные стратегии. Например, если элементы одной строки не больше некоторых выпуклых линейных комбинаций соответствующих элементов других строк, то соответствующую стратегию можно исключить, заменив ее смешанной стратегией с соответствующими частотами использования чистых стратегий.
Рассмотрим пример:
 .
.
Если взять чистую стратегию 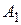 с частотой 0,25, а
с частотой 0,25, а 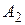 с частотой 0,75, то
с частотой 0,75, то 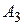 мажорируется линейной комбинацией
мажорируется линейной комбинацией 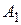 и
и 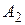 , так как:
, так как:
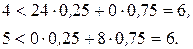
Поэтому стратегию 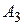 можно исключить.
можно исключить.
Аналогично можно поступать и со стратегиями 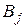 второго игрока.
второго игрока.
Дата добавления: 2015-01-29; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |