Сведение матричной игры к задаче линейного программирования

Рассмотрим матричную игру m×n с платежной матрицей . И будем считать, что все элементы 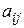платежной матрицы положительны. Этого всегда можно добиться применением аффинного правила, то есть мы можем просто прибавить ко всем элементам матрицы одно и тоже положительное число. Тогда искомая цена игры 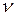будет тоже являться положительным числом.

Начнем с первого игрока. Оптимальная смешанная стратегия первого игрока обеспечивает ему средний выигрыш, не меньший , при любой чистой стратегии второго игрока. То есть будут выполняться неравенства:

Если ввести новые переменные по формуле , то можно получить:

Так как первый игрок стремится максимизировать свой выигрыш , то решение матричной игры можно свести к следующей задаче линейного программирования:

Найти:

, (2.17)

при следующих ограничениях:

(2.18)

Рассмотрим теперь интересы второго игрока. Его оптимальная смешанная стратегия обеспечивает ему средний проигрыш, не больший 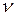, при любой чистой стратегии первого игрока. То есть:

Если ввести новые переменные , то можно получить следующую задачу линейного программирования:

Найти

, (2.19)

при следующих ограничениях:

(2.20)

Таким образом, мы пришли к следующей теореме.

Теорема 2.3. Решение матричной игры с положительной платежной матрицей равносильно решению двойственных задач линейного программирования (2.17) - (2.18) и (2.19) - (2.20). При этом цена игры 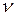- это величина, обратная значению оптимальных сумм:

,

а оптимальные значения и равны

.

Рассмотрим теперь алгоритм решения матричной игры:

1. Ко всем элементам платежной матрицы прибавим одно и тоже положительное число так, чтобы все элементы платежной матрицы стали положительными.

2. Сводим матричную игру к двойственной задаче линейного программирования и находим их решения: .

3. Строим оптимальные смешанные стратегии игроков:

.

4. Вычисляем цену игры

.

№ 2.9.Решить матричную игру из № 2.6 сведением к задаче линейного программирования.

Решение. Сведем матричную игру к двойственной задаче линейного программирования:

(2.21)

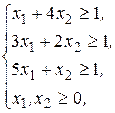(2.22)

- «прямая» задача линейного программирования, и

(2.23)

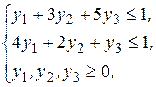(2.24)

- «обратная» задача.

Симплексным методом «легче» решается обратная задача ЛП, так как здесь требуется введение двух дополнительных переменных, против трех в задаче (2.21)-(2.22). Поэтому найдем сначала оптимальную стратегию второго игрока, решив задачу (2.23)-(2.24).

Шаг 1. Введем дополнительные переменные :

Возьмем в качестве основных переменные и , тогда свободными будут переменные :

Получим базисное решение

которое является допустимым, поэтому вычислим значение целевой функции:

Так как в выражении для целевой функции все коэффициенты при переменных – положительны, то в основные можно перевести любую из них. Для этого вычислим:

Следовательно, переводим в основные переменную , а в свободные – переменную .

Шаг 2. Основные переменные: и , свободные: :

Получаем базисное решение:

,

которое является допустимым, поэтому вычисляем значение целевой функции:

Так как в выражении для целевой функции коэффициент при является положительным, то переменную необходимо перевести в основные:

.

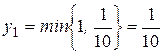Следовательно, в свободные переходит переменная .

Шаг 3. Основные переменные: и , свободные: :

Получаем базисное решение:

,

которое является допустимым, потому вычислим значение целевой функции:

Так как все коэффициенты при переменных в выражении для целевой функции отрицательны, то оптимальное решение задачи (2.23)-(2.24) найдено:

,

Определим теперь оптимальную стратегию второго игрока и цену игры:

а) цена игры:

,

б) оптимальная смешанная стратегия:

, , ,

то есть

.

Чтобы определить оптимальную стратегию первого игрока найдем решение задачи (2.21)-(2.22), воспользовавшись свойствами решений взаимно двойственных задач линейного программирования, а именно:

, .

Следовательно, оптимальная смешанная стратегия первого игрока равна:

, ,

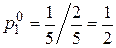то есть

.