РАВНОВЕСНАЯ СИТУАЦИЯ

Как уже отмечалось выше, одной из основных задач теории игр является выработка принципов оптимальности, то есть правил, которые позволяют установить, какое поведение игроков следует считать разумным (целесообразным) с точки зрения самих игроков.

Поскольку все возможные действия игроков в матричной игре описываются множеством стратегий и , то задача заключается в выборе такой стратегии, которая способствует достижению поставленной цели – максимизации выигрыша для игрока или минимизации проигрыша для игрока .

Рассмотрим методику поиска решения на следующем примере матричной игры, повторяемой многократно:

№ 2.3. Найти решение матричной игры :

.

Решение. Попробуем определить оптимальные стратегии игроков. Начнем со стратегии первого игрока, который стремится максимизировать свой выигрыш, учитывая то, что второй игрок будет пытаться свести выигрыш первого игрока к минимуму. Если первый игрок выберет стратегию 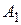, то второй ответит стратегией 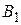, при которой выигрыш первого равен наименьшему значению -2. 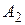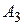На стратегию будет ответом или с минимальным выигрышем 1, а на стратегию - с минимальным выигрышем -3.

Запишем эти минимальные выигрыши в правый столбец:

Таблица 2.1

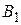
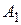
	-2		-1	-2
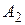
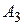
		-3		-3

Естественно, что первый игрок выбирает стратегию 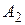, при которой его минимальный выигрыш максимален:

.

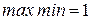Таким образом, если первый игрок выберет стратегию 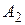, ему гарантирован выигрыш не меньший, чем 1, при любом поведении второго игрока.

Рассмотрим теперь поведение второго игрока. Если он выберет стратегию 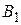, то первый может ответить стратегией 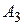, при которой он получит максимальный выигрыш 3, на ответит 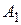, и на - 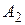или .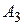

Запишем эти максимальные выигрыши в нижней строке.

Таблица 2.2.

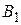
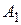
	-2		-1	-2
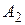
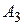
		-3		-3

Естественно, что второй игрок выбирает стратегию , при которой максимальный выигрыш первого игрока минимален:

.

То есть, если второй игрок будет придерживаться стратегии , то при любом поведении первого игрока он не проиграет больше, чем 1.

В этом примере числа и совпали:

.

Это означает, что стратеги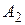и и являются оптимальными стратегиями игроков в том смысле, что при многократном повторении игры, отказ от выбранной стратегии любым из игроков уменьшает его шансы на выигрыш (увеличивает его шансы на проигрыш).

И в самом деле. Если первый игрок будет придерживаться, например, стратегии 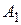, то не стоит думать, что второй этого не заметит. Конечно же заметит и тут же ответит стратегией 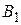и выигрыш первого игрока уменьшится.

Таким образом, мы получили так называемую равновесную ситуацию .

Рассмотрим теперь произвольную матричную игру:

, (2.1)

и опишем общий алгоритм, с помощью которого можно определить, есть ли в этой игре ситуация равновесия. При этом мы предполагаем, что оба игрока действуют разумно, то есть стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим для себя образом.

Рассмотрим действия первого игрока:

1. В каждой строке матрицы находится минимальный элемент:

,

и полученные числа запишем в виде добавочного правого столбца к матрице :

.

То есть, выбирая некоторую стратегию первый игрок рассчитывает выиграть не меньше при любых действиях второго игрока.

2. Среди чисел выбирается наибольшее число:

. (2.2)

То есть, выбрав описанную стратегию (2), первый игрок гарантирует себе выигрыш не меньший . Число (2) называют нижней ценой игры.

Таким образом, действуя наиболее осторожно и рассчитывая на наиболее разумное поведение соперника, первый игрок должен остановиться на той стратегии, при которой число будет максимальным.

Принцип построения стратегии игрока, основанный на формуле (2) называется принципом максимина, а выбранная стратегия называется максиминной стратегией первого игрока.

Рассмотрим теперь поведение второго игрока.

1. В каждом столбце матрицы находится максимальный элемент:

,

и полученные числа запишем в виде нижней добавочной строки:

. (2.3)

То есть, выбрав некоторую стратегию 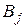, второй игрок рассчитывает на то, что в результате любых действий первого игрока он проиграет не больше .

Среди чисел выбирается наименьшее число

. (2.4)

То есть, выбрав стратегию (4) второй игрок гарантирует себе проигрыш, не превышающий . Число называется верхней ценой игры.

Таким образом, действуя наиболее осторожно и рассчитывая на наиболее разумное поведение соперника, второй игрок должен остановиться на стратегии, при которой будет минимальным.

Принцип построения стратегии второго игрока, основанный на правиле (4), называется принципом минимакса, а выбранная стратегия называется минимаксной стратегией второго игрока.

Отметим, что нижняя и верхняя цена игры всегда связаны соотношением:

. (5)

Если , то ситуация называется равновесной, и ни один из игроков не заинтересован в том, чтобы ее нарушить.

В случае, если , то их общее значение называют ценой игры :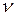

. (6)

В этом случае цена игры 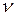совпадет с соответствующим элементом матрицы , который называется точкой равновесия или седловой точкой матрицы . Или, седловой точкой является элемент матрицы , максимальный в своем столбце и минимальный в своей строке.

Стратегии и , соответствующие седловой точке, называются оптимальными, а совокупность пары оптимальных решений и цены игры 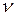называется решением матричной игры с седловой точкой.

Если , то речь пойдет уже об игре без седловой точки. В этом случае предложенный выбор стратегий к равновесной ситуации не приводит, и при многократном повторении игры у игроков могут возникнуть мотивы к нарушению рекомендаций, приведенных выше.

№ 2.4. Найти нижнюю и верхнюю цены игры для следующей матричной игры:

.

Решение. Определим максиминную стратегию первого игрока, выбрав наименьшие значения выигрышей в каждой строке:

.

Определим минимаксную стратегию второго игрока, выбрав наибольшие значения проигрышей для второго игрока в каждом столбце матрицы выигрышей:

.

Здесь уже нет седловой точки, так как .

Допустим, что первому игроку стало известно, что второй игрок принял минимаксную стратегию , тогда оптимальной для первого игрока будет не максиминная стратегия 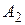, а стратегия 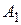, дающая ему выигрыш .

Это означает, что бывают ситуации, когда первый игрок может получить выигрыш, превосходящий максиминный, если ему известны намерения второго игрока (при многократном повторении игры в сходных условиях).