МАТРИЧНЫЕ ИГРЫ m×2

В этом случае платежная матрица игры имеет вид:

.

Решение этой игры аналогично решению игры , только в этом случае на плоскости ищется минимум верхней огибающей прямых

.

Рассмотрим конкретный пример игры .

№ 2.7.Найти решение игры :

.

Решение. 1. Проанализируем игру на наличие седловой точки:

То есть и необходимо применить смешанную стратегию.

2. Вычислим средние выигрыши второго игрока (при условии, что первый игрок выбирает только чистые стратегии). Из таблицы

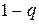
	-2

получаем следующие прямые:

3. Построим верхнюю огибающую.

Рис.2.9

4. Так как наименьшее значение верхней огибающей получается как решение системы уравнений:

то получаем:

,

,

,

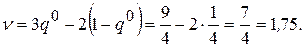
5. Найдем смешанную стратегию первого игрока, полагая , и приравнивая средние выигрыши первого игрока:

,

,

Проверка:

Таким образом, получаем следующее решение игры:

.