
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрическая форма записи комплексных чисел.
Это запись комплексного числа в виде

где r – модуль комплексного числа, j - аргумент.
Примечание: если комплексное число записано в виде
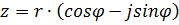 ,
,
то это означает, что угол φ отрицательный и данное число надо записать в виде:

Рис.4.1. Геометрическая интерпретация комплексного числа
Модуль комплексного числа:

Аргументкомплексного числа (j) - величина угла между положительным направлением действительной оси и вектором, соответствующим комплексному числу.
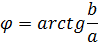
Аргумент зависит от того, в какой координатной четверти лежит вектор, соответствующий этому комплексному числу:
 или
или 
Пример. Перевести число 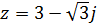 из алгебраической формы записи в тригонометрическую.
из алгебраической формы записи в тригонометрическую.
Решение: a = 3, 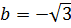
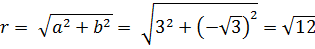
Так как 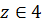 четверти следовательно,
четверти следовательно,

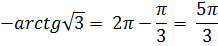
Тогда, тригонометрическая форма записи имеет вид:
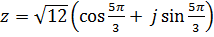 .
.
Действия над комплексными числами в тригонометрической форме: 
1. 
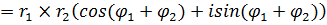
2. 
3.  - формула Муавра
- формула Муавра
Пример.Выполнить действия над комплексными числами в тригонометрической форме:
А) 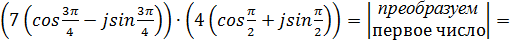
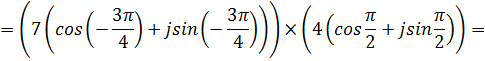
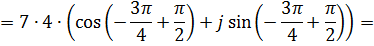
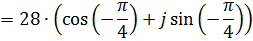
Б) 

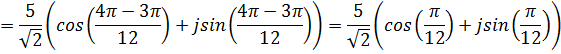
Дата добавления: 2015-02-09; просмотров: 297; Мы поможем в написании вашей работы!; Нарушение авторских прав |