Линейные однородные дифференцируемые уравнения второго порядка с постоянными коэффициентами

Линейным однородным дифференциальным уравнением второго порядка с постоянным коэффициентами называется уравнение:

где р и q – некоторые числа

Для решения такого дифференциального уравнения необходимо составить характеристическое уравнение: Это уравнение имеет два корня.

Возможны три разных случая:

1. Корни характеристического уравнения действительны и различны (дискриминант уравнения ). Тогда общее решение однородного дифференцируемого уравнения будет выглядеть следующим образом:

2. Корни характеристического уравнения действительны и совпадающие (дискриминант уравнения ). Тогда общее решение однородного дифференцируемого уравнения будет выглядеть следующим образом:

или

3. Корни характеристического уравнения комплексные числа: Тогда общее решение дифференцируемого уравнения ищется в виде:

Пример.Найти решение однородного ДУ 2-го порядка:

Решение:

Составим характеристическое уравнение: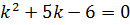

Найдем дискриминант:

Уравнение имеет два разных действительных корня:

значит, решение дифференциального уравнения будет иметь вид:

Пример.Найти решение однородного уравнения:

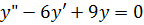
Решение:

Составим характеристическое уравнение:

Найдем дискриминант: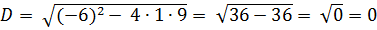

уравнение имеет два совпавших действительных корня:

значит, решение дифференциального уравнения будет иметь вид:

Пример.Найти решение однородного дифференциального уравнения:

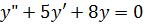
Решение:

Составим характеристическое уравнение:

Найдем дискриминант:

уравнение имеет комплексные корни:

значит, решение уравнения будет иметь вид:

Лекция 10. ЧИСЛОВЫЕ РЯДЫ