Числовые ряды. Признаки сходимости числовых рядов

Пусть задана бесконечная последовательность чисел .

Выражение называется числовым рядом. Числа называются членами этого ряда.

Член ряда, стоящий на n-ом месте, считая от начала, называется общим членом этого ряда. Выражение удобно обозначать следующем образом:

Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда.

Рассмотрим частичные суммы:

Если существует конечный предел , то его называют суммой ряда и говорят, что ряд сходиться.

Если не существует (например , то говорят, что ряд расходиться и суммы не имеет.

Теорема.(Необходимый признак сходимости ряда). Если ряд сходиться, то его n-й член стремиться к нулю при неограниченном возрастании n, то есть

Следствие.Если n-й член ряда не стремиться к нулю ( ), то ряд расходиться.

Рассмотренный признак является только необходимым, но не является достаточным, то есть из того, что n-й член ряда стремиться к нулю, еще не следует, что ряд сходится – ряд может и расходиться.

Достаточные признаки сходимости числовых рядов:

Теорема.(Признак сходимости Даламбера). Если для числового ряда с положительными членами существует предел , то ряд сходится при и расходится при . При ряд может как сходиться, так и расходиться.

Теорема.(Признак Коши). Если для числового ряда с положительными членами существует предел , то ряд сходится при и расходится при . При ряд может как сходиться, так и расходиться.

Теорема.(Интегральный признак Коши). Пусть дан ряд с положительными членами , члены которого являются значениями непрерывной положительной функции f(x) при целых значениях аргумента х: ; , . . . , , … и пусть f(x) монотонно убывает в интервале [1, ∞). Тогда ряд сходится, если сходится несобственный интеграл , и расходится, если этот интеграл расходится.

Таким образом, если , то ряд расходится, если же равен любому конечному числу, то ряд сходится.

Пример: Записать ряд в развернутой форме a₁ + a₂ + … + a_n + … , если задан общий член

Решение:

;

;

;

и т.д.

Таким образом, получим

Пример:Определить сходимость числового ряда

Решение.Воспользуемся необходимым признаком сходимости ряда. Для данного числового ряда записываем формулу общего члена и вычисляем предел:

Так как предел не равен нулю, то исходный ряд расходится.

Пример: Используя признак Даламбера исследовать ряд на сходимость.

Решение: ;

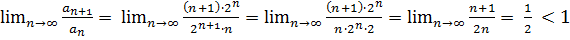. Следовательно, ряд сходится.

Пример: Используя радикальный признак Коши исследовать ряд на сходимость.

Решение:

следовательно, ряд расходится.

Пример 5:Используя интегральный признак Коши исследовать ряд на сходимость.

Решение: ,

так как интеграл не существует, то ряд расходится.