Классическое определение вероятности. Вероятность появления события вычисляется по формуле

Вероятность появления события вычисляется по формуле

где n - число всех элементарных исходов;

m - число исходов, благоприятствующих появлению события .

Свойства вероятности в классической схеме испытаний:

1. Вероятность случайного события есть положительное число, меньше или равное единице.

2. Вероятность достоверного события равна единице.

P(U) = 1

3. Вероятность невозможного события равна нулю.

P(V) = 0

Пример.В урне находятся три одинаковых шара с номерами 1, 2, 3. Найти вероятность того, что извлеченный наугад шар будет с номером 1.

Решение:

Испытание:извлекаем наудачу один шар из трех.

Событие А: извлекаем шар с номером 1.

Р(А) - вероятность того, что извлечен шар под номером 1.

По формуле: , так как , .

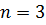Ответ:

Пример. В ящике находится 10 деталей: 8 стандартных и 2 нестандартных. Наудачу вынимаем три детали. Какова вероятность того, что среди этих трех деталей 2 окажутся бракованными?

Решение:

Испытание: Наудачу выбирается три детали из десяти.

Событие А: Среди этих трех деталей 2 окажутся бракованными.

Сформулируем число исходов испытания (n):

Сколькими способами можно выбрать 3 детали из 10?

Подсчитаем число исходов (m), благоприятствующих событию А.

Сколькими способами можно выбрать 2 бракованных и 1 стандартную деталь?

- две бракованных можно выбрать из 2-х деталей: способом;

- одну стандартную можно выбрать из 8 деталей: способами.

Тогда

Р(А) - вероятность того, что среди вынутых трех деталей 2 окажутся бракованными.

.

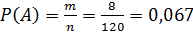Ответ: Р(А) = 0,067.