
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайная величина. Числовые характеристики дискретной и непрерывной СВ.
Случайнойназывают величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной (прерывной) величиной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Законом распределения ДСВ называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| x | x1 | x2 | . . . | хn |
| р | p1 | p2 | . . . | pn |
при этом 
Числовые характеристики ДСВ:
1. Математическое ожидание:

2. Дисперсия:
 или
или 
3. Среднее квадратическое отклонение:

Непрерывной случайной величиной называют случайную величину у которой функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) вычисляется по формуле:
1 способ:  .
.
2 способ: 
Плотностью распределения вероятности НСВ Х называют функцию f(x) - первую производную от функции распределения F(x):

Числовые характеристики НСВ:
1. Математическим ожиданием НСВ Х:

2. Дисперсия НСВ Х:
 или
или 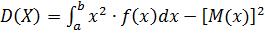
3. Среднее квадратическое отклонение НСВ Х:

Пример. Задана ДСВ Х
| xi | |||
| pi | 0.3 | 0.4 | 0.3 |
Найти: 1) Функцию распределения F(х) ДСВ и построить ее график.
2) M(x), D(x), б(x).
Решение:
1) при x < 2
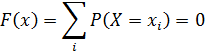
при 2 < x < 5

при 5 < x < 9

при x > 9
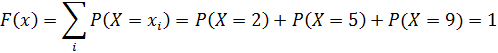
Тогда получим, 
2) найдем числовые характеристики ДСВ:
а) 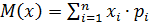 ;
;
M(x)=2 
б)  ;
;


в) 

Пример. НСВ Х задана функцией распределения

Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,2).
Решение:
1способ:
 .
.
2 способ:


Ответ : 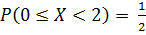 .
.
Пример. Найти математическое ожидание и дисперсию НСВ Х, заданной функции распределения

Решение:
Найдем функцию плотности распределения:
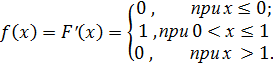
Найдем математическое ожидание по формуле:

Найдем дисперсию по формуле:

Лекция 12. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ
Необходимо заметить, что:
- любое измерение нельзя выполнить абсолютно точно: ошибку дает либо сам прибор, либо наблюдатель;
- счет дает точные результаты, только если количество пересчитываемых предметов невелико и если оно постоянно во времени;
- далеко не все математические операции можно выполнить абсолютно точно.
Поэтому первым в теории численных методов является вопрос о способах определения погрешности данного числа и о приемах определения погрешности чисел, полученных в результате ряда простейших арифметических действий с приближенными числами.
Величина  , где А – точное значение числа,
, где А – точное значение числа,  – его приближенное значение, называется абсолютной погрешностью числа
– его приближенное значение, называется абсолютной погрешностью числа  .
.
Границей абсолютной погрешности (ее предельным значением) называется возможно меньшее число  , про которое известно, что
, про которое известно, что  .
.
На практике мы вынуждены брать число  с запасом, так как точное значение А, как правило, остается неизвестным и, следовательно, невозможно вычислить
с запасом, так как точное значение А, как правило, остается неизвестным и, следовательно, невозможно вычислить  . Знание
. Знание  и
и  позволяет установить границы, в которых лежит точное число А, так как из неравенства
позволяет установить границы, в которых лежит точное число А, так как из неравенства  следует, что
следует, что  .
.
Например, запись  означает, что
означает, что  , или
, или 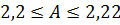 .
.
Замечание 1. Если  есть приближенное значение числа А, причем предельная абсолютная погрешность равна
есть приближенное значение числа А, причем предельная абсолютная погрешность равна  , то говорят, что
, то говорят, что  есть приближенное значение числа А с точностью до
есть приближенное значение числа А с точностью до  .
.
Замечание 2. Известно, что точное значение А некоторого числа находится в интервале  . Тогда, если его приближенное значение
. Тогда, если его приближенное значение  , то предельная абсолютная погрешность этого числа равна
, то предельная абсолютная погрешность этого числа равна  .
.
Пример. Известно, что  .
.
Если взять за приближенное значение числа  число
число  , то предельная абсолютная погрешность равна:
, то предельная абсолютная погрешность равна:  .
.
Таким образом, 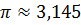 с точностью до 0,005.
с точностью до 0,005.
Однако абсолютная погрешность сама по себе не характеризует точности вычислений, поскольку она выражается в тех же единицах, что и измеряемая величина, и, следовательно, ее значение будет меняться, когда изменяются единицы, с помощью которых мы измеряем изучаемую величину.
Для характеристики точности приближенных вычислений вводят понятие относительной погрешности числа  , являющегося приближенным значением величины А, которая определяется как отношение абсолютной погрешности к абсолютному значению числа
, являющегося приближенным значением величины А, которая определяется как отношение абсолютной погрешности к абсолютному значению числа  , т.е.
, т.е.  .
.
Границей относительной погрешности (ее предельным значением) будем называть возможно меньшее число 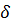 , про которое известно, что
, про которое известно, что
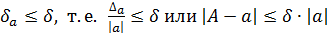 ,
,
откуда следует, что  .
.
В отличие от абсолютной погрешности, относительная погрешность всегда величина безмерная, обычно выражаемая в процентах.
Пример.При измерении длины l и диаметра d некоторого провода получены значения 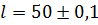 м,
м,  мм. Вычислить границы относительных погрешностей
мм. Вычислить границы относительных погрешностей 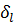 и
и  .
.
Решение:
 ,
, 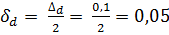
В процентах имеем:  ,
, 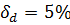
Лекция 13. ОКРУГЛЕНИЕ ЧИСЕЛ. ПОГРЕШНОСТИ ПРОСТЕЙШИХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Округлить число – значит сохранить в нем одну или несколько цифр, считая слева направо, а остальные отбросить.
Значащими цифрами приближенного числа называются все цифры в его записи начиная с первой ненулевой слева.
Цифра в представлении приближенного числа десятичной дробью называется верной, если абсолютная погрешность числа не превосходит единицы того разряда, в котором записана эта цифра. В противном случае она называется сомнительной.
Например, если а = 3,7412 ± 0,002 , то цифра 4 верная, так как  , следовательно, и предыдущие цифры 3 и 7 являются верными; цифра 1 сомнительная, так как
, следовательно, и предыдущие цифры 3 и 7 являются верными; цифра 1 сомнительная, так как  , следовательно и следующая цифра 2 является сомнительной.
, следовательно и следующая цифра 2 является сомнительной.
Правило (правило округления). Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если нужно для сохранения разрядов, заменяют их нулями.
При этом если первая из отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу.
Если же отбрасывается только одна цифра 5, то последнюю из сохраняемых цифр оставляют без изменения, если она четная, и увеличивают на единицу, если она нечетная.
Разряды десятичного числа:
| Х | Х | Х | Х | . | Х | Х | Х | Х |
| тысячи | сотни | десятки | единицы | десятые | сотые | тысячные | десятитысячные |
Пример: Округлить значение числа а = 145,7183 до единиц, сотых, тысячных, сотен.
Решение:
до единиц: а ≈ 146
до сотых: а ≈ 145,72
до тысячных: а ≈ 145,718
до сотен: а ≈ 100
Запись чисел в стандартном виде
Всякое положительное число можно записать в виде
 (*)
(*)
где число a удовлетворяет неравенствам 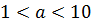 , k - целое число.
, k - целое число.
Если число записано в виде (*), то говорят, что оно записано в стандартном виде. Целое число k называется порядком данного числа.
Например, порядок числа  равен 1, порядок числа
равен 1, порядок числа  равен -2, порядок числа
равен -2, порядок числа  равен 0.
равен 0.
Например, если  и
и  , то
, то 
и следовательно, 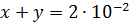 с точностью до
с точностью до  .
.
Аналогично, 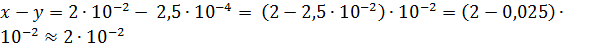 с точностью до
с точностью до  .
.
Если порядок числа x равен n, а порядок числа y равен m, то порядок произведения x∙y равен (n + m) или (n + m + 1).
Например, если  и
и  , тогда
, тогда  и
и  .
.
Погрешности простейших арифметических действий:
Положение 1. Предельная абсолютная погрешность суммы нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей слагаемых.
Замечание. При сложении приближенных чисел в полученном результате нужно отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из данных приближенных чисел.
Пример.Найти сумму  , если
, если  ,
, 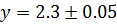
Решение: Из условия задачи следует, что 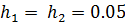 . По правилу подсчёта точности суммы получаем
. По правилу подсчёта точности суммы получаем 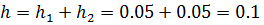 Следовательно,
Следовательно, 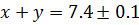 .
.
Положение 2.Предельная абсолютная погрешность разности двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
Замечание. При вычитании приближенных чисел в полученном результате нужно отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из данных приближенных чисел.
Пример. Найти разность  , если
, если  ,
, 
Решение: Из условия задачи следует, что  ,
,  . По правилу подсчёта точности разности имеем
. По правилу подсчёта точности разности имеем  . Следовательно,
. Следовательно,  .
.
Положение 3. Предельная относительная погрешность произведения нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей сомножителей.
Замечание. При умножении приближенных чисел в результате нужно сохранять столько значащих цифр, сколько имеет приближенное данное с наименьшим количеством значащих цифр (самое «короткое» из данных приближенных чисел).
Пример.  ;
; 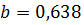 ;
; 
Решение: Будем иметь:
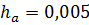 ;
;  .
.
 ;
;  .
.

Но  , откуда
, откуда 
Если округлить число u до приближенного значения  , то получим:
, то получим:
 .
.
Положение 4.Предельная относительная погрешность от деления двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей делимого и делителя.
Замечание.При делении приближенных чисел в результате нужно сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр (самое «короткое» из данных приближенных чисел).
Пример.  ;
;  ;
; 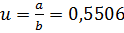
Решение: Будем иметь:
 ;
; 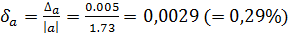 .
.
 ;
; 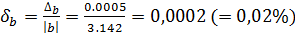 .
.
 .
.
Но  , откуда
, откуда  .
.
Если мы хотим округлить число u до приближенного значения  , то получим:
, то получим: 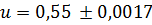 .
.
Положение 5. Предельная относительная погрешность степени приближенного числа, записанного в десятичной форме верными цифрами, равна произведению показателя степени на предельную относительную погрешность основания.
Замечание. При возведении приближенного числа в квадрат и куб в результате нужно сохранять столько значащих цифр, сколько их имеет возводимое в степень число.
Пример. Найти степень  , если
, если 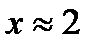 с точностью до 2.5%.
с точностью до 2.5%.
Решение: По правилу подсчёта точности степени получаем  с точностью до
с точностью до  , т. е.
, т. е.  с точностью до 10%.
с точностью до 10%.
Найдём границу абсолютной погрешности степени:  . Следовательно,
. Следовательно, 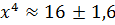 .
.
Положение 6. Предельная относительная погрешность корня из приближенного числа, записанного в десятичной форме верными цифрами, равна предельной относительной погрешности подкоренного числа, деленной на показатель корня.
Замечание. При извлечении квадратного или кубического корня из приближенного числа в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число.
Пример. Найти  , если
, если  с точностью до 2.5%.
с точностью до 2.5%.
Решение: По правилу подсчёта точности корня получаем  с точностью до
с точностью до 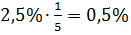 .
.
Найдём границу абсолютной погрешности степени:  . Следовательно,
. Следовательно,  .
.
Лекция 14. МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Численное интегрирование – это вычисление определенного интеграла путем замены подынтегральной функции более простой аппроксимирующей функцией, последующего прямого интегрирования и получения расчетных формул (квадратурных формул).
Геометрический смысл определенного интеграла – это площадь криволинейной трапеции, описываемой подынтегральной функцией
Численные методы нахождения определенного интеграла сводятся к вычислению площади криволинейной трапеции путем замены y=f(x) более простой линией. В зависимости от того, многочленом какой степени заменяется кривая y=f(x), получают различные формулы численного интегрирования: формулы прямоугольников, формулу трапеции, формулу Симпсона.
Рассмотрим график функции y=f(x) на [a;b]. Разобьем [a;b] точками на n равных частей, так что а=х0 < x1 < …< xn=b. Точки х0, х1,…хn – называют узлами разбиения.
Очевидно, что каждая точка  , где k = 1,2,…,n,
, где k = 1,2,…,n,  - шаг.
- шаг.
Формула средних прямоугольников:

Формула средних прямоугольников для расчета:

 Формула левых прямоугольников:
Формула левых прямоугольников:
Формула для расчета:

Формула правых прямоугольников:
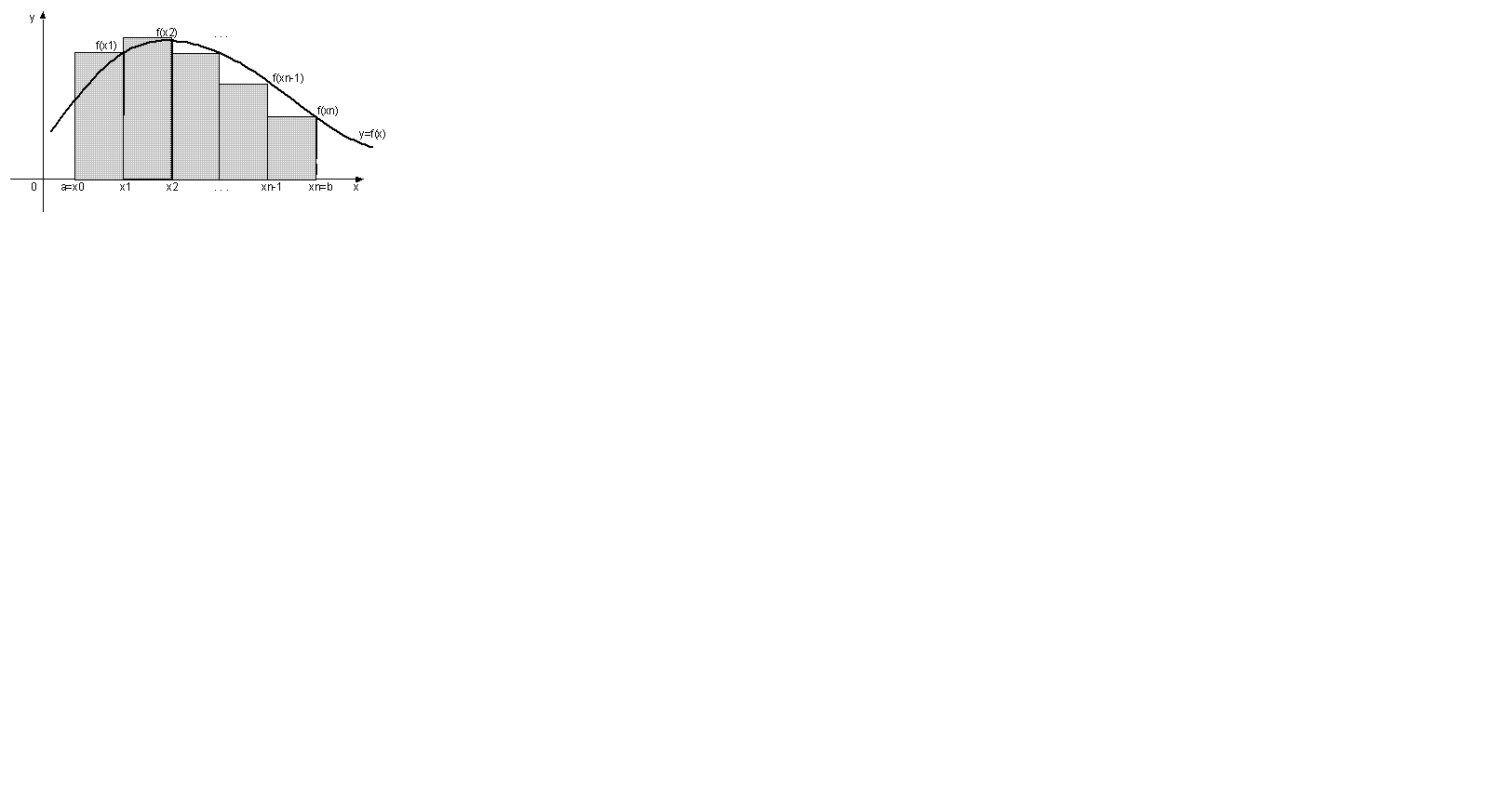
Формула для расчетов:

Формула трапеции:

Формула метода трапеции имеет вид:

 Метод Симпсона (метод парабол):
Метод Симпсона (метод парабол):
Формула для расчетов имеет вид:


Пример.Вычислить определенный интеграл  по формулам прямоугольников и трапеции при n=6,
по формулам прямоугольников и трапеции при n=6,  .
.
Решение: подынтегральная функция имеет вид f(x)=  , a = 0, b = 0.6
, a = 0, b = 0.6
Шаг интегрирования равен 
Так как  и т.д., то составим расчетную таблицу.
и т.д., то составим расчетную таблицу.
Примечание: в связи с тем, что определенный интеграл необходимо вычислить и по формуле средних прямоугольников, то шаг в таблице будет равен  (см. таблицу)
(см. таблицу)
| n | xn | 
| 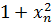
| f( xn)= 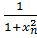
|
| 0,000 | 1,000 | 1,000 | ||
| 0,5 | 0,05 | 0,003 | 1,003 | 0,998 |
| 0,1 | 0,010 | 1,010 | 0,990 | |
| 1,5 | 0,15 | 0,023 | 1,023 | 0,978 |
| 0,2 | 0,040 | 1,040 | 0,962 | |
| 2,5 | 0,25 | 0,063 | 1,063 | 0,941 |
| 0,3 | 0,090 | 1,090 | 0,917 | |
| 3,5 | 0,35 | 0,123 | 1,123 | 0,891 |
| 0,4 | 0,160 | 1,160 | 0,862 | |
| 4,5 | 0,45 | 0,203 | 1,203 | 0,832 |
| 0,5 | 0,250 | 1,250 | 0,800 | |
| 5,5 | 0,55 | 0,303 | 1,303 | 0,768 |
| 0,6 | 0,360 | 1,360 | 0,735 |
Для вычисления определенного интеграла по формуле средних прямоугольников воспользуемся формулой:


Для вычисления определенного интеграла по формуле левых прямоугольников воспользуемся формулой:


Для вычисления определенного интеграла по формуле правых прямоугольников воспользуемся формулой:


По формуле трапеции получим:


Литература:
1. Валуце И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы. М.: Наука, 1980г. – 496с.
2. Григорьев С.Г. Математика: учебник для студ. сред. проф. учреждений / Григорьев С.Г., Задулина С.В.; под ред. Гусева В.А. – М.: Издательский центр «Академия», 2007г.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Учебное пособие для втузов. – 6-е изд., испр. – М. Высш. шк., 2002г.
4. Калиниченко Ю.А. Введение в численные методы: Учебное пособие. – Хабаровск: ХИИК, 2013г.
5. Осипова В.Ю., Калиниченко Ю.А. Учебное пособие «Теория вероятностей», 2001г., - 58с.
6. Пехлецкий И.Д. Математика: Учебник. – М.: Издательский центр «Академия», 2002. – 304с.
7. Филимонова Е.В., Тер-Симонян Н.А. Математика и информатика: Учебное пособие. – М.: Издательско-книготорговый центр «Маркетинг», 2002.- 384с.
8. Шипачев В. С. Задачи по высшей математики. М.: Выс. шк., 1997г. – 304с.
Дата добавления: 2015-02-09; просмотров: 462; Мы поможем в написании вашей работы!; Нарушение авторских прав |