Дифференциальные уравнения первого порядка

с разделяющимися переменными:

А) Если в дифференциальном уравнении y′=f(x,y) функция f(x,y) может быть представлена в виде: , то уравнение называется уравнением с разделяющимися переменными.

Его решение (интегрирование) проводится по следующему алгоритму:

1. Представим , тогда уравнение запишется:

2. Разделить переменные:

3. Проинтегрировать обе части равенства:

,

где С – произвольная постоянная.

Это общий интеграл уравнения, входящие в него неопределенные интегралы находятся методами, рассматриваемыми в интегральном исчислении.

Б) Если дифференциальное уравнение записано в виде:

,

то это уравнение с разделяющимися переменными, если

;

Интегрирование уравнения производится так:

;

Считая , разделим на :

Интегрируя обе части получим:

- общий интеграл уравнения.

Заметим, при разделении переменных могут быть «потерянные» решения, которые в некоторых случаях будут особыми решениями.

Пример: Найти общее решение дифференциального уравнения

Решение:

Так как , то получим

Это дифференциальное уравнение с разделяющимися переменными.

Разделим переменные (у – влево, х - вправо) и получим:

Проинтегрируем обе части дифференциального уравнения:

Рассмотрим решение каждого из интервалов отдельно:

Тогда, получим

Ответ:

Пример: Найти частное решение дифференциального уравнения с разделяющимися переменными, удовлетворяющее начальному условию

при

Решение: , ,
Это дифференциальное уравнение с разделяющимися переменными.

Проинтегрируем обе части дифференциального уравнения:

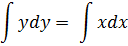
Рассмотрим решение каждого из интервалов отдельно:

Тогда, получим

Чтобы найти частное решение ДУ надо найти значение С при условии, что , :

Тогда частное решение ДУ имеет вид:

Ответ: