
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула Тейлора для функции, не являющейся многочленом
Рассмотрим разложение основных функций в ряд Маклорена:
·  . Для любых действительных значений х функцию
. Для любых действительных значений х функцию  можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена

· 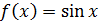 . Для любых действительных значений х функцию
. Для любых действительных значений х функцию  можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена

·  . Для любых действительных значений х функцию
. Для любых действительных значений х функцию  можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена

·  . Для любых действительных значений х функцию
. Для любых действительных значений х функцию  можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена

·  . Для любых действительных значений х функцию
. Для любых действительных значений х функцию 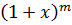 можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена


·  . Для любых действительных значений х функцию
. Для любых действительных значений х функцию  можно представить в виде сходящегося ряда Маклорена
можно представить в виде сходящегося ряда Маклорена

Пример. Разложить в ряд Маклорена следующие функции:
а) 
б) 
Решение:
а) воспользуемся формулой:

сделаем замену 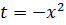

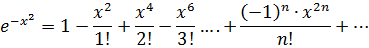
б) Воспользуемся известным соотношением из тригонометрии:
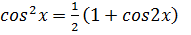 (*)
(*)
Разложение функции  имеет вид:
имеет вид:
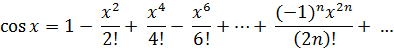
Заменим x в разложении cosx на 2x и получим разложение cos2x:


Найдем разложение  :
:
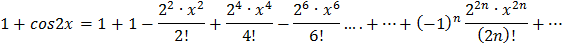
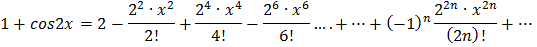
Тогда, разложение 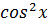 будет иметь вид:
будет иметь вид:
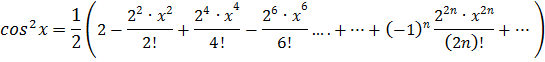

Лекция 11. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Дата добавления: 2015-02-09; просмотров: 289; Мы поможем в написании вашей работы!; Нарушение авторских прав |