
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрическое приложение определенного интеграла (площадь криволинейной трапеции).
Рассмотрим фигуру
Рис. 8.1. Криволинейная трапеция
Фигура, ограниченная снизу отрезком [a; b] оси Ox, сверху графиком непрерывной функции y = f(x) такой, что f (x) ≥ 0 при х  [a; b] и f (x) > 0 при х
[a; b] и f (x) > 0 при х  (а; b), а с боков ограниченная отрезками прямых х = а и x = b, называется криволинейной трапецией.
(а; b), а с боков ограниченная отрезками прямых х = а и x = b, называется криволинейной трапецией.
Отрезок [a; b] называют основанием этой криволинейной трапеций.
Площадь криволинейной трапеции вычисляется по формуле:

Таким образом, геометрический смысл определенного интеграла заключается в вычислении площади криволинейной трапеции.
Приведём различные примеры криволинейной трапеции:

Рассмотрим основные способы вычисления площади криволинейной трапеции:
| Рисунок | Формула |
| |
 
|
|
|
 или
или

|
|
| 

|
| |
S=S1+S2
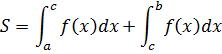
|
Алгоритм нахождения площади криволинейной трапеции:
1. Построить графики функции;
2. Определить пределы интегрирования a и b;
3. Выбрать и записать соответствующую формулу площади криволинейной трапеции;
4. Вычислить площадь криволинейной трапеции.
ПРИМЕР : Вычислить площадь криволинейной трапеции, ограниченной осью Ох, прямыми х = -1, х = 2 и параболой y = 9 - x2.
Решение: Построим график функции y = 9 - x2 и изобразим данную криволинейную трапецию:
y = 9 - x2 -парабола, ветви вниз,
координаты вершины: 

(0 ; 9) - вершина
Точки пересечения с осью Ох:
9 - x2 = 0
-x2 = 9
x2 = 9 => x1/2 =  3
3
Проведём прямые х = - 1 и х = 2
f(x)=9 - x2 a = - 1 b = 2
Формула для вычисления площади криволинейной трапеции:


 .
.
Ответ: Sкр.тр = 24(кв.ед)
Лекция 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дата добавления: 2015-02-09; просмотров: 499; Мы поможем в написании вашей работы!; Нарушение авторских прав |