
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример.
А) 

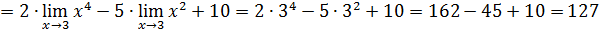
Б) 

В) 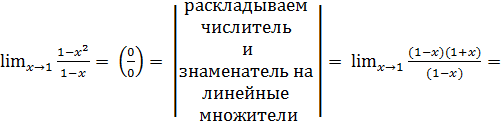
 Г)
Г) 

Д) 




Лекция 6. ПРОИЗВОДНАЯ ФУНКЦИИ
Пусть функция f(x) определена в некоторой окрестности точки x0.
Производной функции f(x) в точке x0 называется предел отношения приращения функции ∆f(x0) к приращению аргумента ∆х, при ∆х→0, если этот предел существует, и обозначается f '(x0).
| ∆y |
| ∆x |
| f(x) f(x0) |
| y=f(x) |
| 0 x0 x x |
| y |
Рис. 6.1. График дифференцируемой функции

Операция нахождения производной называется дифференцированием функции.
Функция, имеющая производную в точке х0, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала (а;b), называется дифференцируемой на этом интервале.
Правила дифференцирования:
Пусть U, V - дифференцируемые функции независимой переменной х , С – константа, тогда:
1) 
2) 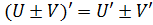
3) 
4) 
Пример.Найти производную функции
А)  ;
;
Б)  ;
;
В)  ;
;
Г) 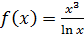 .
.
Решение:
А) 
 .
.
Б) 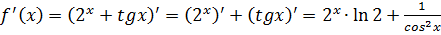 .
.
В) 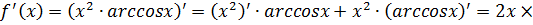
 .
.
Г)  .
.
Дата добавления: 2015-02-09; просмотров: 255; Мы поможем в написании вашей работы!; Нарушение авторских прав |