
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства пределов
1. Предел постоянной равен этой постоянной.
Lim A=A , если А = const
2. Постоянную можно вынести за знак предела.
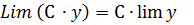 , если С = const
, если С = const
В теории пределов существуют следующие соотношения:
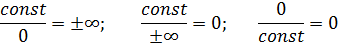
Основные неопределенности:
1. 
Чтобы раскрыть неопределенность  надо числитель и знаменатель разделить на неизвестное в наивысшей степени.
надо числитель и знаменатель разделить на неизвестное в наивысшей степени.
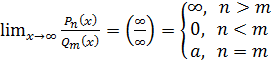 , где
, где
n – наивысшая степень числителя,
m – наивысшая степень знаменателя,
а – отношение коэффициентов при х в наивысшей степени.
2. 
Чтобы раскрыть неопределенность  надо числитель и знаменатель разложить на линейные множители.
надо числитель и знаменатель разложить на линейные множители.
3. 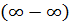
Чтобы раскрыть неопределенность 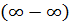 надо домножить и разделить на сопряженное выражение.
надо домножить и разделить на сопряженное выражение.
Замечательные пределы:
Первый замечательный предел:предел отношения sin бесконечно малой величины к самой этой величине равен 1.
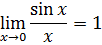
Свойства:
1. 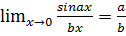
2. 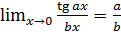
3. 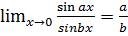
Второй замечательный предел:
 или
или 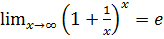
Частный случай:
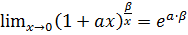 ;
; 
Дата добавления: 2015-02-09; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |