
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экспоненциальная (показательная) форма записи комплексных чисел.
Это запись комплексного числа в виде
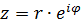 ,
,
где r – модуль комплексного числа, j - аргумент
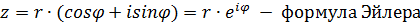
Действия над комплексными числами в показательной форме:
1. 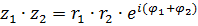
2. 
3. 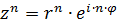
4. 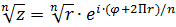
Пример.Выполнить действия над комплексными числами в экспоненциальной (показательной) форме записи:
А) 
Б) 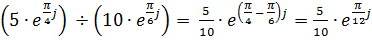
В) 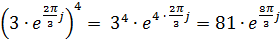
Лекция 5. ПРЕДЕЛ ФУНКЦИИ
Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу А. Тогда говорят, что число А есть предел функции f(x) при x → a.
Число A называется пределом функции f( x ) в точке a , если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a , и для каждого ε > 0 существует δ > 0 такое, что для всех x , удовлетворяющих условию | x – a | < δ, x ≠ a , выполняется неравенство
| f ( x ) – A | < ε.
Если A – предел функции в точке a , то пишут, что
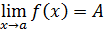
Теоремы о пределах(правила предельного перехода)
1. Предел суммы или разности равен сумме или разности пределов.
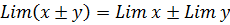
2. Предел произведения равен произведению пределов.

3. Предел отношения равен отношению пределов.
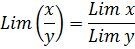
Дата добавления: 2015-02-09; просмотров: 379; Мы поможем в написании вашей работы!; Нарушение авторских прав |