Метод Крамера. Метод Крамера состоит в следующем

Метод Крамера состоит в следующем. Составляется n + 1 определитель:

Δ – определитель системы (составляется из коэффициентов системы в том порядке, как они записаны в системе;

Δ_хi – определители каждого неизвестного (составляются из определителя системы Δ путем последовательной замены столбца коэффициентов того неизвестного, определитель которого записывается, столбцом свободных коэффициентов)

Решение системы находится по формулам Крамера:

х₁ = ; х₂ = ; … х_n = .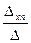

Если Δ = 0, то система либо не имеет решений, либо имеет бесконечное множество решений, которые могут быть найдены методом исключения.

Пример 1. Решить методом Крамера:

Решение. Составим и найдем определитель системы:

Δ = = -12-10= -22

Составим и найдем определитель Δх (заменим столбец коэффициентов при неизвестном х столбцом свободных коэффициентов):

Δх = = -56+100= 44

Найдем определитель Δу (заменим столбец коэффициентов при неизвестном у столбцом свободных коэффициентов):

Δу = = - 60-28= -88

Решением будет: . Ответ: (-2; 4).

Пример 2. Решить систему методом Крамера: .

Решение.Составим и найдем определитель системы:

Δ = = - 27

Составим и найдем определитель Δх (заменим столбец коэффициентов при неизвестном х столбцом свободных коэффициентов):

Δх = = - 81

Вернем первый столбец на место и составим и найдем определитель Δу (заменим столбец коэффициентов при неизвестном у столбцом свободных коэффициентов):

Δу = = - 108

Вернем второй столбец на место и составим и найдем определитель Δz (заменим столбец коэффициентов при неизвестном z столбцом свободных коэффициентов):

Δz = = - 135.

Подставив найденные значения определителей в формулы Крамера, получим:

х = ; у = ; z = .

Ответ:(3; 4; 5 ).