Геометрическое изображение комплексных чисел

Всякое комплексное число z = х + iy можно изобразить точкой М(х; у) плоскости хОу такой, что х = Re z, у = Im z. И наоборот, ка­ждую точку М(х; у) координатной плоскости можно рассматривать как образ комплексного числа z = х + iy.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней ле­жат действительные числа z= х + 0i = х. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные чи­сла z = 0 + iy.

Комплексное число z = x + iy можно задавать с помощью радиус-вектора . Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначает­ся или r.

Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное чи­сло, называется аргументом этого комплексного числа, обозначается Arg z или .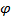

Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа z 0 величина многозначная и определяет­ся с точностью до слагаемого 2 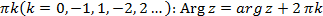где arg z — главное значение аргумента, заключен­ное в промежутке [— ; , т. е. — argz (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2 ]).