
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия над комплексными числами
Сложение комплексных чисел
Суммой двух комплексных чисел z1 = x1 + iy1 и z2 = х2 + iy2 называется комплексное число, определяемое равенством

Например. 
Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число, которое, будучи сложенным с z2, дает число z1, т.е.  , если z+z2=z1
, если z+z2=z1
Если z1 = x1 + iy1 и z2 = х2 + iy2, то из этого определения легко получить z:

Например, 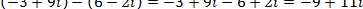
Умножение комплексных чисел
Важнейшее соотношение  .
.
Благодаря ему формально перемножаем двучлены

Например, (2-3i)·(-5+4i)=-10+8i+15i-12i2=-10+23i+12=2+23i
Заметим, что  .
.
Деление комплексных чисел
Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 z2 называется комплексное число z, которое, будучи умноженным на z2, дает число z1, т.е.  , если z2z= z1.
, если z2z= z1.
На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).
Пример. Выполнить деление  .
.
Решение:

Дата добавления: 2015-02-09; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |