Проверьте себя

Вычислить производную:	Ответы:
А)
Б)
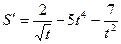
В)
Г)

КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Запишите правило вычисления производной произведения двух функций.

2) Запишите правило вычисления производной частного двух функций.

3) Дополните фразу: «Постоянный сомножитель можно … за знак производной».

4) Выберите из приведённых ниже функций сложную:

А) 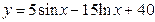Б) В) Г)

Дифференциал функции равен произведению производной функции на дифференциал аргумента. Если функция 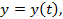то формула дифференциала функции.

Задание.Вычислить дифференциал функции а) б) .

Решение.

Дифференциал функции равен произведению производной функции на дифференциал аргумента. Если функция 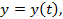то формула дифференциала функции.

а) Найдем производную по правилу производной произведения двух функций:

Воспользуемся формулами: .

Производная будет: .

Подставим в формулу дифференциала: .

б) Найдем производную по правилу производной сложной функции:

.

Получаем дифференциал функции: