Предел функции

Бесконечно большие, бесконечно малые функции

Пусть функция f(x) определена в некоторой окрестности точки x₀.

Определение. Число А называется пределом функции f(x) при x стремящемся к х₀ (или х х₀), если разность между ними ничтожно мала, т.е. Пишут

Если f(x)®0 при х х_0, то функцию f(x) называют бесконечно малой.

Например,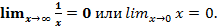

Если f(x)®¥ при х х_0, то функцию f(x) называют бесконечно большой.

Например,

Утверждение. Бесконечно малая и бесконечно большая величины являются взаимообратными, т. е.

Основные теоремы о пределах функций

1.Предел суммы (разности) функций равен сумме (разности) пределов от каждой функции:

2. Предел произведения функций равен произведению пределов от каждой функции:

3. Предел частного двух функций равен частному пределов:

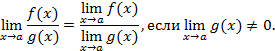
4. Предел постоянной величины равен ей самой. Пусть C=const-постоянная.

5. Постоянный множитель можно выносить за знак предела:

6. Предел степени равен степени предела:

.

Вычисление пределов функций

А) Вычисление предела многочленов. Например,

Таким образом, для вычисления предела многочлена достаточно вместо переменной х подставить значение, к которому она стремится.

Б) Вычисление предела отношения двух многочленов:

В) так как знаменатель стремится к нулю (см. утверждение).

Г) (см. утверждение).

Раскрытие случаев .

Правило 1 (х→ 0). Необходимо в числителе и знаменателе вынести за скобки хв меньшей общей степени, сократить и продолжить поиск предела.

Пример. Найти .

Решение.Вынесем за скобки х в первой (меньшей для числителя и знаменателя) степени, получим:

.

Правило 2 (х→ ). Необходимо в числителе и в знаменателе вынести за скобки х в наибольшей степени.

Пример. Найти .

Решение.Вынесем за скобки х в третьей (большей для числителя и знаменателя) степени, получим:

Указание. Воспользовались свойством:

Правило 3 (х → С, С ≠ 0). Числитель и знаменатель разложить на линейные множители, сократить и продолжить поиск предела.

Пример. Найти - неопределенность.

Решение.Разложив на множители числитель и знаменатель, получим:

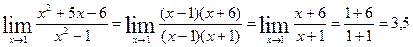
Указания. Формула разложения квадратичной функции на множители:

, где х₁ и х₂ – корни соответствующего уравнения

Тогда

Для знаменателя – формула разности квадратов: 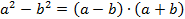,тогда