Производная функции. Дифференциал.

Производная функции y=y(x) определяется по формуле: , где 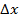– приращение аргумента, приращение функции.

Правила:

1 (С- постоянная)	5
2	6
3	7
4

Формулы

1 1

2 2

3 3

4 4

5 5

6 6

7 7

8 8

9 9

10 10

11 11

Приёмы вычисления производной

Пример 1. Найти производную функции .

Решение: - применим правила (2) и (4)

- по формулам (1), (3) , а так же по правилам (1) и (5) получаем

- после упрощения производная примет вид .

Пример 2. Найти производную функции

Решение: - преобразовать по свойствам степени

- по формуле (3) найти производную при

( воспользовались формулой )

Пример 3. Найти производную функции .

Решение: - по правилу (3) имеем:

- по правилу (6) примет вид:

- после раскрытия скобок производная:

Этот пример можно решить иначе:

- открыть скобки и упростить

- применить правила (2) и(4)

- по формуле (3) и по правилам (1) и (5) получим:

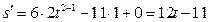
Пример 4. Найти производную функции

Решение: - применить правило (7)

- применить правило суммы (2) и формулу (3) вычисления производной

Пример 5. Найти производную функции

Решение: данная функция является сложной; положим . Согласно формуле (2) , получаем . Применим правила (2) и (4): . По формуле (3) имеем: . После упрощения примет вид: .

Пример 6. Найти производную функции

Решение:

- применить правило (4) и формулу сложной функции (4) , где , тогда