
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Комплексные числа. Понятие комплексного числа.
Понятие комплексного числа.
Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами математики. Сначала для счета предметов использовались натуральные числа. Затем необходимость выполнения деления привела к понятию дробных положительных чисел; далее необходимость выполнения вычитания к понятию нуля и отрицательных чисел, наконец, извлечение корня из положительных чисел – к понятию иррациональных чисел. Остались и невыполненные операции, например, извлечение квадратного корня из отрицательного числа.
Возникает новое понятие – мнимая единица, т.е. 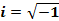 . Это такое число, квадрат которого равен -1, т.е.
. Это такое число, квадрат которого равен -1, т.е.  В технической литературе применяют обозначение
В технической литературе применяют обозначение  . Геометрически действительные числа изображаются точками на координатной прямой. Между ними существует взаимно-однозначное соответствие. На координатной прямой «нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Поэтому естественно в качестве новых чисел – их называют комплексными – ввести упорядоченные пары действительных чисел.
. Геометрически действительные числа изображаются точками на координатной прямой. Между ними существует взаимно-однозначное соответствие. На координатной прямой «нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Поэтому естественно в качестве новых чисел – их называют комплексными – ввести упорядоченные пары действительных чисел.
Комплексным числом называется выражение вида z = х + iy, где х и у — действительные числа, а i — так называемая мнимая единица, i2 = — 1.
Если х = 0, то число 0 + iy = iy называется чисто мнимым; если у = 0, то число х +i0= х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. е. R  C
C
Число х называется действительной частью комплексного числа z и обозначается х = Re z, а у — мнимой частью z, у =  .
.
Два комплексных числа 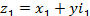 и
и  называются равными (
называются равными (  ) тогда и только тогда, когда равны их действительные части и равны их мнимые части
) тогда и только тогда, когда равны их действительные части и равны их мнимые части 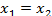 ,
, 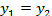 - В частности, комплексное число z=x+iy равно нулю тогда и только тогда, когда х = у = 0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.
- В частности, комплексное число z=x+iy равно нулю тогда и только тогда, когда х = у = 0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Два комплексных числа z = х + iy и 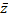 = х — iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
= х — iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
Решение квадратного уравнения
Рассмотрим квадратное уравнение 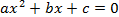 . Из школьного курса математики известно:
. Из школьного курса математики известно:
А) если дискриминант уравнения положителен 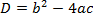 >0, то уравнение имеет два различных действительных корня:
>0, то уравнение имеет два различных действительных корня: 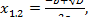
Б)если D=0, то корни совпадают 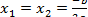 ,
,
В) если D<0,тодействительных корнейнет.
Покажем, что в случае отрицательного дискриминанта уравнение имеет два различных комплексных корня.
Вначале рассмотрим уравнение: 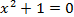


Уравнение имеет корни: 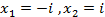 . Получили мнимые корни.
. Получили мнимые корни.
Можно извлекать корни, например, 
Решим уравнение 
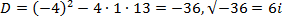
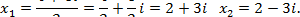
Пример. Решить уравнение 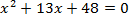
Решение: 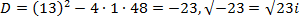
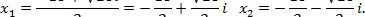
Дата добавления: 2015-02-09; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |