Решение. Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой

Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно:

Т₁ + П₁ = Т₂ + П₂ (1)

где Т₁ , П₁ ,Т₂ , П₂ – кинетическая и потенциальная энергии ракеты после выключения в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях. Согласно определению кинетической энергии:

Т₁ = ½ mv .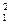

Потенциальная энергия ракеты в начальном состоянии:

П₁ = - GmM/R.

По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая – убывает. В конечном состоянии кинетическая энергия Т₂ станет равна нулю, а потенциальная – достигнет максимального значения:

П₂ = - GmM/(2R).

Подставляя выражения Т₁ , П₁ ,Т₂ , П₂ в (1), получаем: mv 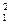/2 - GmM/R = - GmM/(2R), откуда v₁ = .

Заметив, что GM/R² = g (ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде: v₁ = , что совпадает с выражением для первой космической скорости. Произведем вычисления:

v₁ = = 7,9км/с.