Решение. Число N молекул, содержащихся в некоторой системе массой m, равна произведению постоянной Авогадро NА на количество вещества v: N=vNA

Число N молекул, содержащихся в некоторой системе массой m, равна произведению постоянной Авогадро N_А на количество вещества v: N=vN_A

Так как v= m/М, где М – молярная масса, N = . Выразив в этой формуле массу как произведение плотности на объем V, получим: N=ρVN_A/M.

Произведем вычисления, учитывая, что М= 18*10^-3 кг/моль (см. приложение 14):

N = *6,02*10²³ молекул = 3,34*10¹⁹ молекул.

Массу m₁ одной молекулы можно найти по формуле: m₁ = М/ N_А. (1).

Подставив в (1) значения М и N_А, найдем массу молекулы воды:

m₁ = кг = 2,99*10^-26кг.

Если молекулы воды плотно прилегают друг к другу, то можно считать , что на каждую молекулу приходится объем (кубическая ячейка) V₁=d³, где d – диаметр молекулы. Отсюда: d = (2)

Объем V₁ найдем, разделив молярный объем V_m на число молекул в моле, т.е. на N_А:

V₁ = V_m/ N_А. (3)

Подставим выражение (3) в (2):

d = ,

где V_m = М/ρ. Тогда: d = 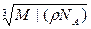(4)

Проверим, дает ли правая часть выражения (4) единицу длины:

= 1 м.

Произведем вычисления:

d= 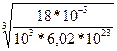м = 3,11*10^-10м = 311пм.

Пример 4.

В баллоне объемом 10л находится гелий под давлением р₁ = 1Мпа и при температуре Т₁ = 300К. После того как из болона было взято m = 10г гелия, температура в болоне понизилась до Т₂ = 290К. Определить давление р₂ гелия, оставшегося в болоне.

Решение.

Для решения задачи воспользуемся уравнением Менделеева – Клайперона, применив его к конечному состоянию газа:

р₂V = RT₂. (1)

где m₂ – масса гелия в баллоне в конечном состоянии; М- молярная масса гелия; R- молярная газовая постоянная.

Из уравнения (1) выразим искомое давление:

р₂= mRT₂/(MV). (2)

массу m₂ гелия выразим через массу m₁, соответствующую начальному состоянию, и массу m гелия, взятого из баллона: m₂ = m₁ – m. (3)

Массу m₁ гелия найдем также из уравнения Менделеева- Клапейрона, применив его к начальному состоянию: m₁ = Мр₁V/(RT₁) (4)

Подставив выражения массы m₁ в (3), а затем выражение m₂ в (2), найдем:

р₂ = .

или

Р₂ = р₁ - . (5)

Проверим. дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них дает единицу давления, так как состоит из двух множителей, первый из которых (Т₂/Т₁) –безразмерный, а второй – давление. Проверим второе слагаемое:

= = =1Па.

Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М = 4*10^-3 кг/моль (см. приложение 14) :

р₂ = Па =3,64*10⁵ Па = 0,364 Мпа.