Решение. Рассмотрим систему пружина – пуля

Рассмотрим систему пружина – пуля. Так как на теле системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия Е₁ системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е₂ в конечном состоянии (когда пуля поднялась на высоту h), т.е.:

Е₁ = Е₂, или Т₁ + П₁ = Т₂+ П₂,

где Т₁, П₁ ,Т₂, П₂ – кинетические и потенциальные энергии системы в начальном и конечном состояниях.

Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид:

П₁ = П₂ (2)

Примем потенциальную энергию.

Пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е. П₁ = ½ kx², а в конечном состоянии- потенциальной энергии пули на высоте h, т.е. П₂ = mgh.

Подставив выражения П₁ и П₂ в формулу (2), найдем ½ kx² = mgh., отсюда :

k= 2 mgh/х² .

проверим, дает ли полученная формула единицу жесткости k. Для этого в первую часть формулы (3) вместо величин подставим их единицы:

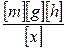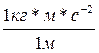= = = 1 Н/м.

Убедившись, что полученная единица является единицей жесткости (1Н/м), подставим в формулу (3) значения величин и произведем вычисления:

k= 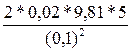Н/м = 196 Н/м.