КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения а
 |
Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения а
, направленного по касательной к траектории, и нормального ускорения ап , направленного к центру кривизны траектории (рис.1): а = а + ап.
Так как векторы а и ап взаимно перпендикулярны, то модуль ускорения:
а = 
(1)
Модули тангенциального и нормального ускорение точки вращающегося тела выражаются формулами: а = εr, ап = ω2r,
где ω – модуль угловой скорости тела; ε – модуль его углового ускорения.
Подставляя выражения а и ап. в формулу (1), находим:
а = 
= r 
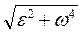
(2)
Угловую скорость ω найдем, взяв первую производную угла поворота по времени:
= В + 2Сt.
В момент времени t = 4с модуль угловой скорости: ω= [20+2 (-2) 4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени: ε = dω/dt = 2C = -4 рад/с2.
Подставляя значения ω, ε и r в формулу (2), получаем:
а = 0,1 
м/с = 1,65 м/с2
Дата добавления: 2015-02-10; просмотров: 123; Мы поможем в написании вашей работы!; Нарушение авторских прав |