Средняя путевая скорость

ВОЛЖСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ВОДНОГО ТРАНСПОРТА

(Казанский филиал)

ФИЗИКА

Методические указания и

контрольные задания для студентов инженерно-технической

специальности заочного обучения

2014г.

ЧАСТЬ 1. Физические основы классической механики.

Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x.

Х = f (t),

где f (t) – некоторая функция времени.

Проекция средней скорости на ось х

[v_x] =

Средняя путевая скорость

[v] =

где Δ_S – путь, пройденный точкой за интервал времени Δ _t. Путь Δ_S в отличие от разности координат Δ_х = х₂ – х₁ не может убывать и принимать отрицательные значения, т.е. Δ_S ≥ 0.

Проекция мгновенной скорости на ось х:

v_x = .

Проекция среднего ускорения на ось х:

(а_х) = .

Проекция мгновенного ускорения на ось х: а_х = .

.

Кинематическое уравнение движения материальной точки по окружности

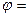f (t), r = R=const.

Модуль угловой скорости

Модуль углового ускорения

=

Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

v = ωR, а = R, а_п = ω²R,

где v – модуль линейной скорости; а и а_п - модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε – модуль углового ускорения; R – радиус окружности.

Модуль полного ускорения: а = , или а = R

Угол между полным а и нормальным а_п ускорениями: = arc cos (а_п /а).

Импульс материальной точки массой m , движущейся со скоростью v, Р = mv.

Второй закон Ньютона: dp = F dt,

где F – результирующая сила, действующая на материальную точку.

Силы, рассматриваемые в механике:

а) сила упругости: F = -кx,

где к – коэффициент упругости (в случае пружины- жесткости); х- абсолютная деформация;

б) сила тяжести: Р = mg;

в) сила гравитационного взаимодействия:

F = G ,

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля: F = mG;

г) сила трения (скольжение): F = f N,

где f – коэффициент трения; N – сила нормального давления.

Закон сохранения импульса:

или для двух тел (i = 2): m₁v₁ + m₂ v₂ = m₁u₁ + m₂u₂,

где v₁ и v₂ – скорость тел в момент времени, принятый за начальный;

u₁ и u₂ – скорости тех же тел в момент времени, принятый за конечный.

Кинетическая энергия тела, движущегося поступательно,

Т = mv²/2, или Т = р²/ (2m).

Потенциальная энергия:

а) упругодеформированной пружины :

П = ½ кх²,

где к – жесткость пружины; х – абсолютная деформация;

б) гравитационного взаимодействия:

П= - Gm₁ m₂ / r,

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);

в) тела, находящегося в однородном поле силы тяжести:

П = mgh,

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедливости при условии h < R, где R – радиус Земли).

Закон сохранения механической энергии: Е = Т + П = соnst.

Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

А = ΔТ = Т₂ – Т₁.

Основные уравнение динамики вращательного движения относительно неподвижной оси Z : М_z = J_z ε,

где М_z – результирующий момент внешних сил относительно оси Z, действующих на тело; ε – угловое ускорение; J_z – момент инерции относительно оси вращения.

Момент инерции некоторых тел массой m относительно оси Z, проходящей через центр масс:

а) стержня длиной t относительно оси, перпендикулярной стержню,

J_z = 1/12 mt²;

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра), J_z = mR²,

где R – радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска:

J_z = 1/2 mR²;

Проекция на ось Z момента импульса тела, вращающегося относительно неподвижной оси Z: L_z = J_z ω ,

где ω – угловая скорость тела.

Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси Z: J_z ω = соnst,

где J_z – момент инерции системы тел относительно оси Z; где ω – угловая скорость вращения тел системы вокруг оси Z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси Z:

Т = ½ J_z ω², или Т = L / (2J_z)