Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия {ε1}= kT, где k – постоянная Больцмана; Т- термодинамическая температура

На каждую степень свободы молекулы газа приходится одинаковая средняя энергия {ε₁}= kT, где k – постоянная Больцмана; Т- термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная)соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода:

{ε_Вр} = 2* kT. (1)

Кинетическая энергия вращательного движения всех молекул газа:

Е_к = {ε_Вр}N. (2)

Число всех молекул газа:

N = N_Аv, (3)

где N_А – постоянная Авогадро; v – количество вещества.

Если учесть, что количество вещества v = m/M, где m – масса газа; М – молярная масса газа, то формула (3) примет вид: N = N_А .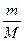

Подставив выражение N в формулу (2), получим:

Е_к = N_Аm{ε_Вр}/М (4)

Произведем вычисления, учитывая, что для кислорода М = 32*10^-3кг/моль (см. табл.14 приложения): {ε_Вр} = kT = 1,38*10^-23*350Дж = 4,83*10^-21Дж;

Е_к = 6,02*10²³* *4,83*10^-21Дж = 364Дж.