Основные формулы.

Связь магнитной индукции В с напряженностью Н магнитного поля:

В = μμ₀ Н,

где μ – магнитная проницаемость изотропной среды; μ₀ – магнитная постоянная. В вакууме μ = 1, и тогда магнитная индукция в вакууме:

В = μ₀ Н,

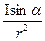Закон Био – Савара – Лапласа: dB [dlr] или dB = dI,

где dB – магнитная индукция поля, создаваемого элементом провода длиной dl с током I; r – радиус – вектор, направленный от элемента проводника к точке в которой определяется магнитная индукция; α – угол между радиусом – вектором и направлением тока в элементе провода.

Магнитная индукция в центре кругового тока: В = ,

где R – радиус кругового витка.

Магнитная индукция на оси кругового тока: B = ,

Где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока: В = μμ₀ I/ (2πr₀),

Где r₀ – расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (см. рис. 31, а и пример 1)

B = 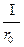(соsα₁ – соsα₂).

Обозначения ясны из рисунка. Направление вектора магнитной индукции В обозначено точкой – это значит, что В направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рис. 31 б), - соsα₂ = соsα_{1 =} соsα, тогда : B = 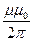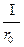соsα.

Магнитная индукция поля соленоида:

В = μμ₀ nI,

где n – отношение числа витков соленоида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера),

F = I [lB], или F = IBlsinα,

Где l – длина провода; α – угол между направлением тока в проводе и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:

DF = I [dlB].

Магнитный момент плоского контура с током: р_m = n/S,

Где n – единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,

М = [p_mB], или М = p_mB sinα,

Где α – угол между векторами p_m и B.

Потенциальная энергия (механическая) контура с током в магнитном поле: П_мех = - p_mB, или П_мех = - p_mB соsα.

Отношение магнитного момента p_m к механическому L (моменту импульса) заряженной частицы, движущейся по кругу орбите, = ,

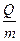Где Q – заряд частицы; m – масса частицы.

Сила Лоренца: F = Q [vB], или F = Qυ B sinα ,

Где v – скорость заряженной частицы; α – угол между векторами v и В.

Магнитный поток:

А) в случае однородного магнитного поля и плоской поверхности6

Ф = BScosα или Ф = B_п S,

Где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции;

Б) в случае неоднородного поля и произвольной поверхности: Ф = В_п dS

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток): Ψ = NФ.

Это формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению замкнутого контура и в магнитном поле: А = IΔФ.

ЭДС индукции: ℰ_i = - .

Разность потенциалов на концах провода, движущегося со скоростью v в магнитном поле, U = Blυ sinα,

Где l – длина провода; α – угол между векторами v и В.

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:

Q = ΔФ/R, или Q = NΔФ/R = ΔΨ/R,

Где R – сопротивление контура.

Индуктивность контура: L = Ф/I.

ЭДС самоиндукции: ℰ_s = - L .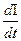

Индуктивность соленоида: L = μμ₀ n² V,

Где п – отношение числа витков соленоида к его длине; V – объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью :

А) I = 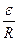(1 – е^-Rt\L) (при замыкание цепи),

где ℰ - ЭДС источника тока; t – время, прошедшее после замыкания цепи;

Б) I = I₀е^-Rt\L (при размыкании цепи), где I₀ – сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.

Энергия магнитного поля: W = .

Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)

W = ВН/2, или w = В²/(2 μμ₀), или w = μμ₀ Н²/2,

Где В – магнитная индукция; Н – напряженность магнитного поля.

Кинематическое уравнение гармонических колебаний материальной точки: х = А соs (ωt + φ),

Где х – смещение; А – амплитуда колебаний; ω – угловая или циклическая частота; φ – начальная фаза.

Скорость ускорения материальной точки, совершающей гармонические колебания: υ = -Aω sin (ωt + φ); : υ = -Aω² соs (ωt + φ);

Сложение гармонических колебаний одного направления и одинаковой частоты:

А) амплитуда результирующего колебания:

А =

Б) начальная фаза результирующего колебания:

φ = arc tg .

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях: х = А₁ соs ωt; y = А₂ соs (ωt + φ):

А) y = 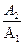х, если разность фаз φ = 0;

Б) y = - 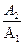х, если разность фаз φ = ±π;

В) 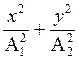= 1, если разность фаз φ = ± .

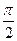Уравнение плоской бегущей волны: у = А соs ω (t - ),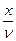

Где у – смещение любой из точек среды с координатой х в момент t;

Υ – скорость распространение колебаний в среде.

Связь разности фаз Δφ колебаний с расстоянием Δх между точками среды, отсчитанным в направлении распространения колебаний;

Δφ = 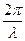Δх,

Где λ – длина волны.