
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Для решение задач воспользуемся законом Био – Савара – Лапласа и принципом суперпозиции магнитных полей
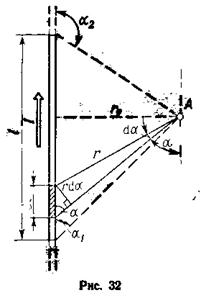
Для решение задач воспользуемся законом Био – Савара – Лапласа и принципом суперпозиции магнитных полей. Закон Био – Савара – Лапласа позволят определить магнитную индукцию dB, создаваемую элементом тока Idl. Заметим, что вектор dB в точке А направлен на плоскость чертежа. Принцип суперпозиции позволяет для определения В воспользоваться геометрическим суммированием 9 интегрированием):
В = 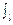 dB, (1)
dB, (1)
Где символ l означает, что интегрирование распространяется на всю длину провода.
Запишем закон Био – Савара – Лапласа в векторной форме:
dB = 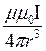
 [dlr],
[dlr],
где dB – магнитная индукция, создаваемая элементом провода длиной dl с током I в точке, определяемой радиусом –вектором r; μ – магнитная проницаемость среды, в которой находится провод (в нашем случае μ = 1*); μ0 – магнитная постоянная. Заметим, что векторы dB от различных элементов тока сонаправлены (рис. 32), поэтому выражение (1) можно переписать в скалярной форме: В = 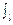 dB,
dB,
где dB = 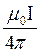
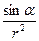 dl.
dl.
В скалярном выражении закона Био – Савара – Лапласа угол α есть угол между элементом тока Idl и радиусом-вектором r. Таким образом:
B = 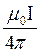
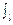
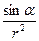 dl. (2)
dl. (2)
Преобразуем подынтегральное выражение так, чтобы была одна переменная – угол α. Для этого выразим длину элемента провода dl через угол dα: dl = rdα / sinα (рис. 32).
Тогда подынтегральное выражение 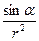 dl запишем в виде :
dl запишем в виде :
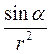
 =
=  . Заметим, что переменная r также зависит от α, (r = r0/sin α); следовательно,
. Заметим, что переменная r также зависит от α, (r = r0/sin α); следовательно, 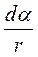 =
= 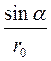 dα.
dα.
Таким образом, выражение (2) можно переписать в виде:
В = 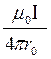
 sinα dα.
sinα dα.
Где α1 и α2 – пределы интегрирования.
 |
Выполним интегрирование: В =
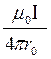 (cosα1 – cosα2). (3)
(cosα1 – cosα2). (3)
Заметим, что при симметричном расположении точки А относительно отрезка провода cosα2 = - cosα1. С учетом этого формула (3) примет вид:
В = 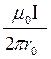 cosα1. (4)
cosα1. (4)
Из рис. 32 следует: cosα1 = 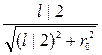 =
= 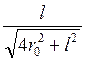 .
.
Подставив выражения cosα1 в формулу (4), получим:
В = 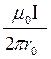
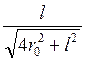 . (5)
. (5)
Произведя вычисления по формуле (5), найдем: В = 26,7 мкТл.
Направление вектора магнитной индукции В поля, создаваемого прямым током, можно определить по правилу буравчика (правилу правого винта). Для этого проводим силовую линию (штриховая линия на рис. 33) и по касательной к ней в интересующей нас точке проводим вектор В. Вектор магнитной индукции В в точке А (рис. 32) направлен перпендикулярно плоскости чертежа от нас.
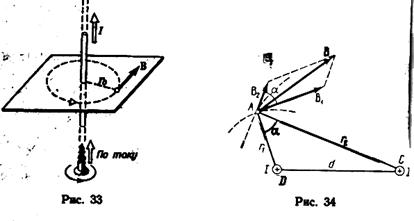
Рис. 33, 34
Пример 2.
Два параллельных бесконечных длинных провода D и C, по которым текут в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию в поля, создаваемого проводниками с током в точке А (рис. 34), отстоящей от оси одного проводника на расстоянии r1 = 5 см, от другого – r2 = 12 см.
Решение.
Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций В1 и В2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
В = В1 + В2.
Модуль вектора В может быть найдем по теореме косинусов:
В = 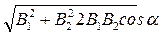 , (1)
, (1)
Где α – угол между векторами В1 и В2 .
Магнитные индукции В1 и В2 выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А:
В1 = μ0I /(2πr1); В2 = μ0I /(2πr2).
Подставляя выражения В1 и В2 в формулу (1) и вынося μ0I /(2π) за знак корня, получаем:
В = 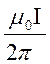
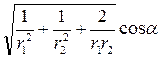 . (2)
. (2)
Вычислим cosα. Заметив, что α = 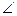 DAC (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем:
DAC (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем:
d2 = r 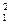 +
+ 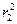 - 2r1 r2 соs α.
- 2r1 r2 соs α.
Где d – расстояние между проводами. Отсюда :
соs α = 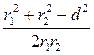 ; соs α =
; соs α = 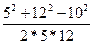 =
= 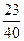 .
.
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:
В = 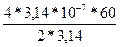
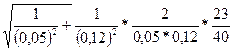 Тл = 3,08*10-4 Тл = 308 мкТл.
Тл = 3,08*10-4 Тл = 308 мкТл.
Пример 3.
По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию В в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.
Дата добавления: 2015-02-10; просмотров: 601; Мы поможем в написании вашей работы!; Нарушение авторских прав |