Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I1 и I2

В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I₁ и I₂, определяется выражением В = В₁ +В₂, где В₁- магнитная индукция поля, создаваемого в точке А током I₁; В₂ – магнитная индукция поля, созданного в точке А током I₂.

Заметим, что векторы В₁ и В₂ взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис. 39). Тогда модуль вектора В можно определить по теореме Пифагора: В= │В│ = ,

Где В₁ и В₂ определяется по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:

В₁ = 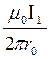и В₂ = .

В нашем случае r₀ = d/2. Тогда: В = .

Проверка единиц величин аналогична выполненной в примере 3.

Проведем вычисления:

Пример 6.

Бесконечно длинный провод изогнут так, как это изображено на рис. 40. Радиус R дуги окружности равен 10 см. Определить магнитную индукцию В поля, создаваемого в точке О током I = 80А, текущим по этому поводу.

Решение.

Магнитную индукцию В в точке О найдем, используя принцип супер позиции магнитных полей: В = ΣB_i. В нашем случае провод можно разбить на три части (рис. 41): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда:

В = В₁ + В₂ + В₃,

Где В₁ , В₂ , В₃ – магнитные индукции в точке О, создаваемые током, текущим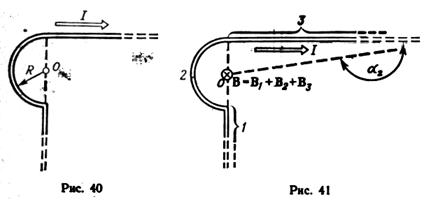
Рис.40 и 41 ,

Так как точка О лежит на оси провода 1, то В₁ = 0 и тогда: В = В₂ + В₃ .

Учитывая что векторы В₂ и В₃ направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим: В = В₂ + В₃ .

Магнитную индукцию В₂ найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока: В = .

В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому: : В = .

Магнитную индукцию В₃ найдем, воспользовавшись соотношением (3), выведенным в примере 1: В = 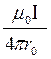(cosα₁ – cosα₂).

В нашем случае r₀ = R, α₁ = π/2 (cosα₁ = 0), α₁ →π 2 (cosα₁ = -1). Тогда:

В = .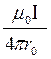

Используя найденные выражения для В₂ и В₃, получим:

В = В₂ + В₃ = + ,

Или

В = (π + 1).

Проверка единиц величин аналогична выполненной в примере 3.

Произведем вычисления:

В = Тл = 3,31*10^-4Тл,

Или В = 331мкТл.

Пример 7.

По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друг, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.

Решение.

Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод.

Предположим, что оба тока (обозначим их для удобства I₁ и I₂) текут в одном направлении. Ток I₁ создает в месте расположения второго провода (с током I₂) магнитное поле.

Проведем линию магнитной индукции (пунктир на рис. 42) через второй провод и по касательной к ней – вектор магнитной индукции В₁. Модуль магнитной индукции В₁ определяется соотношением:

В = 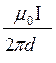. (1)

Рис.42.

Согласно закону Ампера, на каждый элемент второго провода с током I₂ длиной dl действует в магнитной поле сила:

dF = I₂B₁dl sin (dlB).

Так как вектор dl перпендикулярен вектору В₁, то sin (dlB) = 1 и тогда:

dF = I₂B₁dl.

Подставив в это выражение В₁ согласно (1), получим:

dF = dl.

Силу F взаимодействия проводов с током найдем интегрированием:

F = dl = l.

Заметив, что I₁ = I₂ = I, получим: F = .

Убедимся в том, что правая часть этого равенства дает единицу силы (Н):

=1Н.

Произведем вычисления: F = Н = 2,5Н.

Сила F сонаправлена с силой dF (рис.42) и определяется (в данном случае проще) правилом левой руки.

Пример 8.

Протон, прошедший ускоряющую разность потенциалов U = 600В, взлетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.

Решение.

Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной индукции v В. Так как сила Лоренца перпендикулярно вектору v ,то она сообщит частице (протону) нормальное ускорение а_п.

Согласно закону Ньютона:

Fл = m а_п (1)

Где m –масса протона.

Рис. 43.

На рис. 43 совмещена траектория протона с плоскостью чертежи и дано (произвольно) направление вектора v. Силу Лоренца направим перпендикулярно вектору v к центру окружности (векторы а_пи Fлсонаправлены). Используя правило левой руки, определим направление магнитных силовых линий ( направление вектора В).

Перепишем выражение (1) в скалярной форме ( в проекции на радиус):

Fл = m а_п (2)

В скалярной форме Fл= QυBsin α. В нашем случае v Ви sin α.= 1, тогда Fл= QυB. Так как нормальное ускорение а_п = υ²/R, то выражение (2) перепишем следующим образом: QυB = mυ² / R.

Отсюда находим радиус окружности: R = mυ / (QB).

Заметив, что mυ есть импульс протона (р), это выражение можно записать в виде:

R = р/ (QB). (3)

Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = ΔT, или Q(φ₁ - φ₂) = Т₂ – Т₁,

Где φ₁ - φ₂ – ускоряющая разность потенциалов (или ускоряющее напряжение U); Т₂ и Т₁ – начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией протона (Т₁ ≈0) и выразив кинетическую энергию Т₂ через импульс р, получим:

Q U = р²/(2m).

Найдем их этого выражения импульс р = и подставим его в формулу (3):

R = ,

или

R = (4)

Убедимся в том, что правая часть равенства дает единицу длины (м):

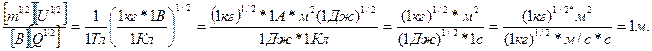
подставим в формулу (4) числовые значения физических величин и произведем вычисления:

R = 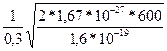м = 0,0118м = 11,8 мм.

Пример 9.

Электрон, влетев в однородное магнитное поле (В = 0,2 Тл), стал двигаться по окружности радиуса R = 5см. определить магнитный момент р_m эквивалентного кругового тока.