Решение. Как известно, на контур с током в магнитном поле действует момент силы рис.48

М = р_m В sin φ, (1)

Где р_m = IS = Iа² – магнитный момент контура; В – магнитная индукция; φ – угол между векторами р_m (направлен по нормали к контуру) и В.

По условию задачи в начальном положении контур свободно установился в магнитное поел. При этом момент силы равен нулю (М = 0), а значит, φ = 0, т.е. векторы р_m и В сонаправлены. Если внешние силы выведут из положения равновесия, то возникший момент сил (см. 1) будем стремится возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменной (зависит от угла поворота φ), то для подсчета работы применим формулу работы в дифференциальной форме dА = Мdφ. Учитывая форму (1), получаем:

dА = IВа² sin φdφ.

Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

А = IВа² sin φdφ. (2) (2)

Работа при повороте на угол φ₁ = 90⁰

А₁ = IВа² sin = IВа² |(-cosφ)| 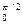= IВа². (3)

Выразим числовые значения величин в единицах СИ (I = 100А, В = 1Тl, а = 10см = 0,1м) и подставим в (3):

А₁ = 100*1*(0,1)² Дж = 1Дж.

Работа при повороте на угол φ₂ = 3⁰ . В этом случае, учитывая, что угол φ₂ мал, заменим в выражении (2) sin φ ≈ φ :

А₂ = IВа² 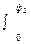φdφ = IВа² φ (4)

Выразим угол φ₂ в радианах. После подстановки числовых значений величин в (4) найдем:

А₂ = 100*1*(0,1)²*(0,0523)²Дж = 1,37*10^-3Дж = 1,37мДж.

Задачу можно решить и другими способами:

1. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур:

А = -IΔФ = I (Ф₁ – Ф₂),

Где Ф₁ – магнитный поток, пронизывающий контур до перемещения; Ф₂ – то же, после перемещения.

Если φ₁ = 90⁰, то Ф₁ = ВS, Ф₂ = 0. Следовательно,

А = IВS = IВа²,

Что совпадает с (3).

2. Воспользуемся выражением для механической потенциальной энергии контура с током в магнитном поле: П(φ) = - р_m В cosφ.

Тогда работа внешних сил: А = ΔП = П₂ – П₁,

Или

А = р_m В(cosφ₁ – cosφ₂).

Так как р_m = Iа², cosφ₁ = I и cosφ₂ = 0, то А = IВа², что также совпадает с (3).

Пример 15.

Соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4А магнитный поток Ф = 6мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида.

Решение.

Индуктивность L связана с потокосцеплением Ψ и силой тока I соотношением:

Ψ = LI. (1)

Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N (при условии, что витки плотно прилегают друг к другу):

Ψ = NФ. (2)

Из формул (1) и (2) находим индуктивность соленоида:

L = NФ/I. (3)

Энергия магнитного поля соленоида: W = ½ LI² .

Выразив L согласно (3) получим: W = ½ NФI. Подставим в формулы (3) и (4) значения физических величин и произведем вычисления:

L = Гн = 1,8*10^-3Гн = 1,8мГн;

W = *1,2*10³*6*10^-6*4Дж = 1,44*10^-2Дж = 14,4мДж.

Пример 16.

Точка совершает гармонические колебания с частотой υ = 10Гц. В момент, принятый за начальный, точка имела максимальное смещение: х_мак = 1 мм. Написать уравнение колебаний точки и начертить их график.

Решение.

Уравнение колебаний точки можно записать в виде:

х = А sin (ωt + φ₁), (1)

Где А – амплитуда колебаний; ω – циклическая частота; t – время; φ₁ – начальная фаза.

По определению амплитуда колебаний: А = х_mах. (2)

Циклическая частота ω связана с частотой υ соотношением:

ω = 2πυ. (3)

Для момента времени t = 0 формула (1) примет вид :

х_mах = А sin φ₁

откуда начальная фаза:

φ₁ = arc sin(х_mах/А) = arc sin 1,

или

φ₁ = (2k+1) π/2 (k = 0,1,2.....).

изменение фазы на 2π не изменяет состояния колеблющей точки, поэтому можно принять:

φ₁ = π/2. (4)

С учетом равенств (2) – (4) уравнение колебаний примет вид:

х = А sin (2πυt + φ), или х = А cos 2πυt,

где А = 1 мм = 10^-3м, υ = 10Гц, φ = π/2.