Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани

Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отраженные пучки света когерентны. Поэтому на поверхности клина будут наблюдается интерференционные полосы. Так как угол клина мал, то отраженные пучки 1 и 2 света (рис. 60) будут практически параллельны. Темные полосы видна на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:

Δ = (2k + 1) λ/2, (k = 0, ± 1, ± 2,...). (1)

Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dn cos ε ) и половины длины волны λ/2 представляет собой добавочную разность хода, возникающую при отражении световой волны 1 от оптически более плотной среды. Подставляя в формулу (1) разность хода Δ световых волн, получаем:

2 d_kn cos ε₂ + λ/2 = (2k + 1) λ/2, (2)

где п – показатель преломления стекла (п = 1,5); d_k – толщина клина в том месте, где наблюдается темная полоса , соответствующая номеру k ; ε₂ - угол преломления.

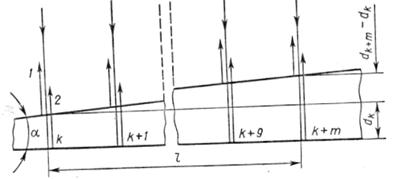
Рис, 60

Согласно условию, угол падения равен нулю; следовательно, и угол преломления ε₂ равен нулю, а cos ε₂ = 1.

Раскрыв скобки в правой части равенства (2), после упрощения получим:

2 d_kn = k λ. (3)

Пусть произвольной темной полосе k-го номера соответствует толщина d_k клина, а темной полосе k + m-го номера – толщина d_k+m клина. Тогда (рис.60), учитывая , что m полос укладывается на расстоянии l, найдем:

Sin α = (d_k+m - d_k)/ l. (4)

Выразим из (3) d_k и d_k+m и подставим их в формулу (4). Затем, учитывая, что

Sin α = α (из –за малости угла α), получим:

α = .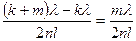

Подставляя значение физических величин, найдем

α = 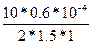рад = 2*10^-4 рад.

Выразим α в секундах. Для этого можно воспользоваться соотношением между радианом и секундой: 1 рад = 206 265". Тогда:

α = 2*10^-4*2,06*10⁵" = 41,2".

Пример 3.

На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2мкм. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного (λ₁ = 0,7 мкм) и в случае фиолетового (λ₂ = 0,41 мкм) света.

Решение.

Из формулы, определяющей положение главных максимумов дифракционной решетки, найдем порядок m дифракционного максимума:

m = (d sinφ)/ λ, (1)

где d – период решетки; φ – угол дифракции; λ – длина волны монохроматического света. Так как sinφ не может быть больше 1, то число m не может быть больше d/ λ, т.е.

m ≤ d/ λ. (2)

подставив в формулу (2) значение величин, получим:

m ≤ 2/0,7 = 2,86 (для красных лучей);

m ≤ 2/0,41 = 4,88 (для фиолетовых лучей).

если учесть, что порядок максимумов является целым числом, то для красного света m _mах = 2 и для фиолетового m _mах = 4.

Пример 4.

Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света образует угол φ = 97⁰ с падающем пучком (рис.61). определить показатель преломления п₁ жидкости, если отраженный свет максимально поляризован.

Рис. 61