Основные формулы. Скорость света в среде:

Скорость света в среде:

υ = с/п,

Где с- скорость света в вакууме; п – показатель преломления среды.

Оптическая длина пути световой волны:

L = nl,

Где l – геометрическая длина пути световой волны в среде с показателем преломления п.

Оптическая разность хода двух световых волн:

Δ = L₁ – L₂.

Зависимость разности фаз от оптической разности хода световых волн:

Δ φ = 2π ,

Где λ – длина световой волны.

Условие максимального усиления света при интерференции:

Δ = ± kλ (k = 0,1,2,.....)

Условие максимального ослабления света:

Δ = ± (2k + 1) .

Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки,

Δ = 2d .

Или Δ = 2dп cos i₂ ± ,

Где d – толщина пленки; п – показатель преломления пленки; i₁ – падения; i₂ – угол преломления света в пленке.

Радиус светлых колец Ньютона в отраженном свете:

r_k = (k = 1.2.3.......)

где k – номер кольца; R – радиус кривизны.

(4)

Радиус темных колец Ньютона в отраженном света:

r_k =

Угол φ отклонение лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия:

а sinφ = (2k + 1)λ/2 (k = 0,1.2.3.......).

где а – ширина щели; k- порядковый номер максимума.

Угол φ отклонение лучей, соответствующий максимуму (светлая полоса) при дифракции решетке, определяется из условия:

d sinφ = ± kλ (k = 0,1,2,3.....),

где d – период дифракционной решетки.

Разрешающая способность дифракционной решетки:

R = λ/Δλ = kN,

Где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ + Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – полное число щелей решетки.

Формула Вульфа – Брэггов:

2 d sinΘ = kλ,

где Θ – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскости в кристалле);

d – расстояние между атомными плоскостями кристалла.

Закон Брюстера:

tgε_в = п₂₁,

где ε_в – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; п₂₁ – относительный показатель преломления второй среды относительно первой.

Закон Малюса:

I = I₀ cos² α,

Где I₀ – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; α – угол между направлением колебаний электрического вектора света, падающего на анализатора (если колебания электрического вектора падающего света совпадают с плоскостью, то анализатор пропускает данный свет без ослабления).

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

А) φ = αd (в твердых телах),

Где α – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;

Б) φ = [α]ρd (в растворах),

Где [α] – удельное вращение; ρ – массовая концентрация оптически активного вещества в растворе.

Релятивистская масса:

m = 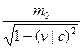, или m = ,

где m₀ – масса покоя частицы; υ – ее скорость; с – скорость света в вакууме; β – скорость частицы, выраженная в далях скорости света (β = υ/с).

Взаимосвязь массы и энергии релятивистской частицы:

Е = m с² , или Е = = ,

Где Е₀ = m₀ с² – энергия покоя частицы.

Полная энергия свободной частицы: Е = Е₀ + Т,

Где Т – кинетическая энергия релятивистской частицы:

Т = (m – m₀)с² , или Т = Е₀ (

Импульс релятивистской частицы:

р= , или р = m₀ с .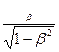

Связь между полной энергией и импульсом релятивистской частицы:

Е² = Е +(рс)².

Закон Стефана – Больцмана: R_е = σТ⁴,

Где R_е – энергетическая светимость (излучательность) абсолютно черного тела; σ – постоянная Стефана – Больцмана ; Т – термодинамическая температура Кельвина.

Закон смещения Вина: λ_m= b/Т,

Где λ_m – длина волны, на которую приходится максимум энергии излучения; b – постоянная Вина.

Энергия фотона:

ε= hυ, или ε = ћω,

где h – постоянная Планка; ћ - постоянная Планка, деленная на 2π; υ – частота фотона; ω – циклическая частота.

Масса фотона: m = ε/c² = h/ (cλ),

Где с – скорость света в вакууме; λ – длина волны фотона.

Импульс фотона: р = m с = h/λ.

Формула Эйнштейна для фотоэффекта:

hυ = А + Т_mах = А + mυ² _mах /2,

где hυ – энергия фотона, падающего на поверхность металла; А – работа выхода электрона; Т_mах – максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта:

υ₀ = А/ h, или λ₀ = hс/А,

где υ₀ – минимальная частота света, при которой еще возможен фотоэффект;

λ₀ – максимальная длина волны света, при котором еще возможен фотоэффект; h – постоянная Планка; с – скорость света в вакууме.

Формула Комптона:

Δλ = λ^' – λ = (1- cos Θ)

Или

Δλ = λ^' – λ =2 sin² ,

Где λ – длина волны фотона, встречавшегося со свободным или слабосвязанным электроном; λ^' – длина волны фотона, рассеянного на угол Θ после столкновения с электроном; m₀ – масса покоящегося электрона.

Комптоновская длина волны:

Λ = h/ (m₀ с) (Λ = 2,436 пм).

Давление света при нормальном падении на поверхность:

р = Е_е (1 + ρ) /с = w (1 + ρ),

где Е_е – энергетическая освещенность (облученность); w – объемная плотность энергии излучения; ρ – коэффициент отражения.

Примеры решения задач.

Пример 1.

От двух когерентных источников S₁ и S₂ (λ = 0,8 мкм) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку (п = 1,33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min пленки это возможно?

Решение.

Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн, т.е.:

Δ₂ – Δ₁ = (2k + 1) λ/2, (1)

Где Δ₁ – оптическая разность хода пучков световых волн до внесения пленки; Δ₂ - оптическая разность хода тех же пучков после внесения пленки;

k = 0, ± 1, ± 2,...

Наименьшей толщине d_min пленки соответствует k = 0.

При этом формула (1) примет вид:

Δ₂ – Δ₁ = λ/2, (2)

Выразим оптические разности хода Δ₂ – Δ₁ . Из рис. 59 следует:

Δ₁ = l₁ – l₂ l_1,

Δ₂ = [ (l₁ - d_min ) + п d_min] – l₂ = (l₁ – l₂ ) + d_min (п – 1).

Подставим выражения Δ₂ и Δ₁ в формулу (2):

(l₁ – l₂ ) + d_min (п – 1) - (l₁ – l₂ ) = λ/2,

или

d_min (п – 1) = λ/2.

Отсюда

d_min = λ/[2 (п – 1) ].

Произведем вычисления:

d_min = мкм = 1,21 мкм.