Пример. 17

Частица массой m = 0,01кг совершает гармонические колебания с периодом Т = 2с. полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F_mах, действующий на частицу.

Решение.

Для определение амплитуды колебаний воспользуемся выражением полной энергии частицы: Е = ½ mω² А² ,

Где ω = 2π/Т. Отсюда амплитуда:

А = , (1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -kx , где k – коэффициент квазиупругой силы; х – смещение колеблющей точки. Максимальной сила будет при максимальном смещении х_mах, равно амплитуде:

F_mах = kА. (2)

Коэффициент k выразим через период колебаний:

k= mω² = m*4π²/Т. (3)

Подставив выражения (1) и (3) в (2) и произведя упрощение, получим:

F_mах = 2π .

Произведем вычисления:

А = 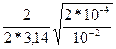0,045м = 45 мм.

F_mах = Н = 4,44*10^-3Н = 4,44мН.

Пример 18.

Складываются два колебания одинакового направления, выражение уравнениями:

х₁ = А₁ cos (t+τ₁ )_; х₂ = А₂ cos (t+τ₂)_;

где А₁ = 3см, А₂ = 2см, τ₁ = 1/6с, τ₂ = 1/3с, Т = 2с.

построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение.

Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой – либо момент времени. Обычно векторную диаграмму строят для времени t = 0. Преобразовав оба управления к канонической форме х = А cos (ωt + φ), получим

х₁ = А₁ cos ( t + τ₁); х₁ = А₂ cos ( t + τ₂);

отсюда видно, что оба складываемых гармоничных колебания имеют одинаковую циклическую частоту:

ω = 2π/Т.

Начальные фазы первого и второго колебаний соответственно равны:

φ ₁ = τ₁; φ ₂ = τ₂;

Произведем вычисления:

ω = = с^-1 = 3,14с^-1;

φ ₁ = 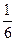рад = 30⁰; φ ₂ = рад = 60⁰;

Изобразим векторы А₁ и А₂ . для этого отложим отрезки длиной А₁ = 3см и А₂ = 2см под углами φ ₁ = 30⁰ и φ ₂ = 60⁰ к оси Ох. Результирующее колебание будет происходить с той же частотой ω и амплитудой А, равной геометрической сумме амплитуд А₁и А₂ : А = А₁+ А₂. Согласно теореме косинусов: А = .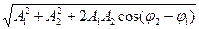

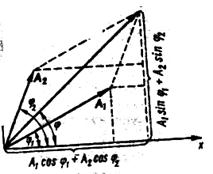
Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис.6)

φ = arctg

Произведем вычисления:

А = = 4.84;

φ = arctg 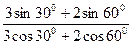= arctg 0,898 = 42⁰,

или φ = 0,735 рад.

Так как результирующие колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде:

х = А cos (ωt + φ),

Где А = 4,84 см, ω = 3,14 с^-1, φ = 0,735 рад.