Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Оу была бы симметрично расположена относительно концов дуги

Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Оу была бы симметрично расположена относительно концов дуги (рис.17). На нити выделим элемент длины dl. Заряд dQ = τdl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность dЕ поля, создаваемого зарядом dQ:

dE =

где r – радиус-вектор, направленный от элемента dt к точке, в которой вычисляется напряженность.

Выразим вектор dE через проекции dE_х и dE_у на оси координат: dE = i dE_х +j dE_у,

где i и j – единичные векторы направлений (орты).

Напряженность Е найдем интегрированием:

Е = 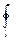dE = i 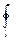dE_х+ j 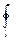dE_у.

Интегрирование ведется вдоль дуги длиной l. В силу симметрии 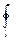dE_х = 0. Тогда:

Е = j 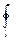dE_у, (1)

где dE_у = dEсоs = τdlcos 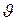/(2πε_оr²). Так как r=R=const, dt = Rd 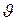, то:

dE_у = соs = соs d .

Подставим выражение dE_у в (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до π/3, а результат удвоим:

Е = j 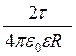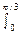соs d = j .

Выразив радиус R через длину l нити (3 l = 2πR), получим:

Е = j . (2)

Из этой формулы видно, что напряженность поля по направлению совпадает с осью Оу.

Найдем потенциал электрического поля в точке О. Сначала найдем потенциал dφ, создаваемый точечным зарядом dQ в точке О:

dφ = τdl/(4πε_о r).

Заменим r на R и проведем интегрирование:

φ = dl =

так как l =2πR/3, то: φ = τ/(6ε_о). (3)

произведем вычисления по формулам (2) и (3):

Е = В/м = 2,18 кВ/м,

φ = В = 188В.