Решение. Совместим координатную плоскость хОу с плоскостью кольца, а ось Оz - с осью кольца (рис

Совместим координатную плоскость хОу с плоскостью кольца, а ось О_z - с осью кольца (рис. 14). На кольце выделим малый участок длиной dl. Так как заряд dQ = τdl , находящийся на этом участке, можно считать точечным, то напряженность dЕ электрического поля, создаваемого этим зарядом, может быть записаны в виде:

dЕ = .

где r – радиус-вектор, направленный от элемента dl к точке А.

Разложим вектор dl на две составляющее: dЕ₁, перпендикулярно плоскости кольца (сонаправленную с осью O_z), и dЕ₂, параллельную плоскости кольца (плоскости хОу) т.е.

dЕ = dЕ₁ + dЕ₂

напряженность Е электрического поля в точки А найдем интегрированием:

Е = ∫_LЕ₁ + ∫_LЕ₂

где интегрирование ведется по всем элементам заряженного кольца. Затем, что для каждой пары зарядов dQ и dQ^'(dQ = dQ^'), расположенных симметрично относительно кольца, векторы dЕ₂ и dЕ^'₂ в точке А равны по модулю и противоположены по направлению: dЕ₂ и -dЕ^'₂. Поэтому векторная сумма (интеграл)

∫_L dЕ₂ = 0. Составляющие dЕ₁ для всех элементов кольца сонаправлены с осью О_z (единичным вектором k), т.е. dЕ₁ = k dЕ₁.

Тогда:

Е = k dE.

Так как dE = , r = и соs = (R/2)/r = 1/ , то dE₁ = .

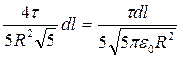Таким образом, Е = k = k .

Из соотношения Q = 2πRτ определим радиус кольца: R= Q/(2πτ). Тогда:

Е = k = k .

Модуль напряженности:

|E| =

проверим, дает ли правая часть полученного равенства единицу напряженности (В/м):

1В\м.

Выразим физические величины, входящие в форму (1), в единицах СИ (τ = 5*10^-8Кл/м, Q = 4*10^-8Кл, ε₀ = 8,85*10^-12 Ф/м) и произведем вычисления:

Е = В/м = 7,92 кВ/м.