Решение. Заметим, что точки, в которых требуется найти напряженность электрического поля, лежит в трех областях (рис.15): области 1 (r1<R1)

Заметим, что точки, в которых требуется найти напряженность электрического поля, лежит в трех областях (рис.15): области 1 (r₁<R₁), области II (R₁< r₂<R₂), области III (r₃<R₃).

1. для определения напряженности Е_r в области I проведем гауссову поверхность S₁ радиусом r₁ и воспользуемся теоремой Остроградского-Гаусса: 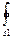E_ndS = 0

(так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю). Из соображений симметрии E_n = E₁ = coпst. Следовательно, E₁ 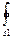dS = 0 и E₁ (напряженность поля в области I ) во всех точках, удовлетворяющих условию r₁<R_1, будет равна нулю.

Рис.15.

2. В области II гауссову поверхность проведем радиусом r₂. В этом случае

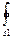E_ndS = Q₁/ε₀,

(так как внутри гауссовой поверхности находится только заряд Q₁).

Так как E_n = E = coпst, то Е можно вынести за знак интеграла:

E 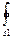dS == Q₁/ε₀, или ЕS₂ = Q₁/ε₀.

Обозначив напряженность Е для области II через Е₂, получим: Е₂ = Q₁/(ε₀ S₂),

где S₂ =4 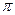r²₂ - площадь гауссовой поверхности. Тогда Е₂ = (1)

2. В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность Е области III через Е₃ и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен Q₁ + Q₂. Тогда Е₃ = .

Заметив, что Q₂ < 0, это выражение можно переписать в виде

Е₃ = . .(2)

Убедимся в том, что правая часть равенства (1) и (2) дает единицу напряженности:

1В\м.

Выразим все величины в единицах СИ (Q₁ = 10^-9 Rk. Q₂ = -0.5*10^-9Кл, r₁ = 0,09м, r₂ = 0,15м, 1/(4πε_о) = 9*10⁹м/Ф) и произведем вычисления:

Е₂ = 9*10⁹ В/м = 1,11кВ/м;

Е₃ = 9*10⁹ В/м = 200В/м

Построим график Е(r). В области 1 (r₁<R₁) Е = 0. В области II (R₁< r<R₂) Е₂ (r) изменяется пот закону 1/r². В точке r = R₁ напряженность Е₂ (R₁) = Q₁/(4πε_о R 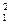)= 2,5 кВ/м. В точке r = R₂ (r стремится к R₂ слева) Е₂ (R₂)= Q₁/(4πε_о R )=0,9 кВ/м. В области III (r<R₂) Е₃ (r) изменяется по закону 1/r², причем в точке r = R₂ (r стремится к R₂ справа) Е₃ (R₂)= Q₁ - |Q₂|/(4πε_о R )= 0,45 кВ/м. Таким образом, функция Е(r) в точках r = R₁ и r = R₂ терпит разрыв.

График зависимости Е_r представлен на рис.16.