
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. Имитационное моделирование является в настоящее время важной частью процесса проектирования сложных технических систем
Имитационное моделирование является в настоящее время важной частью процесса проектирования сложных технических систем. Кроме того, оно широко используется при изучении сложных природных и общественных явлений.
Зачастую реальные объекты не могут быть достаточно адекватно описаны аналитической моделью, которая поддается численному анализу. В этих случаях обращаются к имитационному моделированию. При построении модели определяют множество условий, при которых изучается поведение объекта, и множество числовых характеристик, по значениям которых судят о поведении объекта. Целью изучения объекта при моделировании является, в большинстве случаев, получение функциональных зависимостей между числовыми характеристиками объекта и условиями его функционирования.
В имитационной модели ядром является алгоритм функционирования объекта для всего набора заданных условий. Поэтому в сравнении с аналитической моделью имитационная модель менее абстрактна, содержит больше информации о реальном объекте. При имитационном моделировании не решается математическая задача с целью нахождения функциональных зависимостей, а имитируются условия работы, отдельные действия и события, сопровождающие функционирование моделируемого объекта. При этом искомые функциональные зависимости строятся поточечно в процессе моделирования.
В данном пособии рассматривается один класс имитационных моделей – модели систем массового обслуживания. Данные модели описывают большое количество социальных, экономических и технических систем. Система массового обслуживания (СМО) производит обработку поступающих в неё заявок. Обработка заявок осуществляется обслуживающими устройствами, количество которых в общем случае не ограничено. Если на момент поступления заявки все обслуживающие устройства заняты, то заявка временно помещается в буфер. Как правило, буфер может хранить ограниченное число заявок (см. рис. 1).

Рис. 1 Структурная схема системы массового обслуживания
Для описания СМО как правило используется система обозначений Кендалла, согласно которой простейшая СМО описывается четырехразрядным кодом. Первый разряд обозначает вид закон распределения интервалов между поступлением заявок, второй – закон распределения времени, необходимого для обслуживания заявки. Причем, экспоненциальный закон распределения обозначается буквой M, эрланговское распределение k-го порядка - символом Ek, постоянная величина – буквой D и произвольное распределение буквой - G. Третий разряд обозначает число обслуживающих устройств, а четвертый – объем буфера (если объем буфера считается бесконечным, то четвертый разряд не указывается). Например, система с экспоненциальным законом распределения интервалов между заявками и детерминированным временем обслуживания заявки с одним обслуживающим устройством и буфером, способным хранить 100 заявок, обозначается как M/D/1/100.
В первой лабораторной работе рассматриваются вопросы точности нахождения искомых величин методом имитационного моделирования. Во второй – способы формирования случайных величин с заданным законом распределения. Третья лабораторная работа посвящена моделированию входного потока заявок СМО. Четвертая и пятая – моделированию СМО как таковых с конечным и бесконечным объемами буфера.
Лабораторная работа №1
Вычисление определенных интегралов методом Монте-Карло
1. Необходимые теоретические сведения.
1.1 Введение
История данного метода началась в 1949 году, когда вышла в свет работа Н. Метрополиса и С. Улэма «Метод Монте-Карло». Примечательно происхождение этого названия. Для использования данного метода необходим генератор случайных чисел с равномерным законом распределения. В те годы одной из популярных схем такого генератора была вращающаяся стрелка, которая раскручивалась с большой скоростью и в определенный момент времени останавливалась. Число, на которое она указывала, являлось показанием генератора (см. рис. 2). Такая конструкция напомнила авторам метода рулетку, и он был назван в честь города казино и игорных домов.
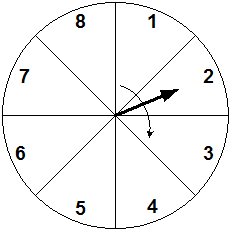
Рис. 2. Генератор-рулетка
Суть метода заключается в формировании случайного процесса, статистические характеристики которого соответствуют искомым величинам решаемой задачи. Например, необходимо определить среднее значение M случайной величины α, для которой плотность распределения вероятностей имеет сложный вид. Аналитическое решение данной задачи может оказаться весьма трудоемким. Возможно решение методом Монте-Карло: для этого берется выборка значений случайной величины αi,  (N – число испытаний). Оценка
(N – число испытаний). Оценка  величины αi будет тогда равна:
величины αi будет тогда равна:

то есть среднему арифметическому выборки.
Наибольшее применение метод Монте-Карло получил в тех областях, где требуется исследовать характеристики случайных процессов. Примерами могут служить: анализ систем массового обслуживания (СМО), прогноз состояния рынка ценных бумаг, оценка надежности различных систем (технических, социальных, экономических) и т.д. Также данный метод применим для решения дифференциальных уравнений, систем линейных алгебраических уравнений, нахождения многомерных интегралов от сложных функций и т. п.
1.2 Точность метода Монте-Карло
Для анализа точности метода Монте-Карло можно использовать закон больших чисел. При моделировании события Х, имеющего вероятность появления p, существует два исхода: событие произошло, и событие не произошло. Пусть xi = 1, если в i-ом опыте событие произошло, и xi = 0, если событие не произошло. Если в N опытах событие Х произошло L раз, то

Найдем математическое ожидание и дисперсию для частоты появления события Х (для величины  ). Математическое ожидание каждого
). Математическое ожидание каждого  равно
равно

Дисперсия каждого xi равна

Тогда математическое ожидание частоты события X равно:

Дисперсия частоты события Х равна:

Согласно теореме Бернулли для всякого ε > 0 и δ > 0 всегда найдется такое число опытов, что частота события Х, равная  , будет отличаться от вероятности этого события p больше, чем на δ, с вероятностью меньшей, чем ε, то есть:
, будет отличаться от вероятности этого события p больше, чем на δ, с вероятностью меньшей, чем ε, то есть:

Применим формулу Чебышева для случайной неотрицательной величины Х, имеющей математическое ожидание MX и дисперсию DX:

Сопоставив формулы (1.1) и (1.2), можно увидеть, что  . Тогда
. Тогда

Приведенная оценка является достаточно грубой, однако она демонстрирует тот факт, что точность метода Монте-Карло имеет порядок 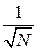 . Например, для десятикратного увеличения точности, приходится увеличивать число опытов в сто раз. Это является существенным ограничением в использовании метода, однако развитие вычислительной техники и наличие большого количества задач, не требующих высокой точности, со временем ослабляют это ограничение.
. Например, для десятикратного увеличения точности, приходится увеличивать число опытов в сто раз. Это является существенным ограничением в использовании метода, однако развитие вычислительной техники и наличие большого количества задач, не требующих высокой точности, со временем ослабляют это ограничение.
Вычисление определенных интегралов методом Монте-Карло
Простейший способ
Рассмотрим случай, когда интегрируемая функция f(x) ограничена на всем интервале интегрирования, то есть c ≤ f(x)≤ d для любого a ≤ x ≤ b (см. рис. 3)

Рис. 3. Пример интегрируемой функции
Тогда определенный интеграл от f(x) в диапазоне от a до b будет равен разности площадей фигур, ограниченных осью абсцисс и кривой и лежащих в верхней и нижней полуплоскостях:

Пусть задан генератор случайных точек в прямоугольнике ACDE c равномерной двумерной плотностью вероятности:

Сформируем с помощью этого генератора N случайных точек (x1, y1), (x2, y2), …, (xN, yN) в прямоугольнике ACDE. Из геометрического рассмотрения видно, что если в фигуру FBG попало N- точек, то площадь ее может быть приближенно найдена из соотношения

Аналогично получается формула

Таким образом, искомый интеграл будет приблизительно равен

Формула (1.3) может быть применена для любой ограниченной функции f(x) при условии, что N- - число точек, для которых выполняется соотношение

а N+ - число точек, для которых выполняется соотношение:

1.3.2. Вычисление с повышенной точностью
Пусть x - случайная величина, равномерно распределенная в интервале (a, b) с плотностью вероятности

Тогда математическое ожидание функции f(x) будет равно:
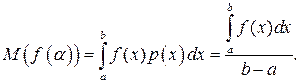
Пусть сформированы N случайных чисел α1, α 2,…, α N с плотностью вероятности p(α). Тогда, математическое ожидание величины f(α) может быть приближенно оценено следующим образом:

Сопоставив формулы (1.4) и (1.5), можно вывести формулу для оценки определенного интеграла 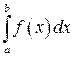 :
:

Оценка (1.6) является более точной, нежели оценка (1.3). Её достоинством также является то, что априорное знание о границах подынтегральной функции не является обязательным.
2. Цель работы
Изучение метода Монте-Карло, определение точности вычисления определенных интегралов методом Монте-Карло.
3. Порядок выполнения работы
1. Записать математически анализируемую функцию. Для этого необходимо из таблицы 1 в соответствии с вариантом выбрать три функции: f1(t), f2(t) и f3(t) (в таблице записаны номера функций, сами функции приведены под таблицей), а также три весовых коэффициента: a1, a2 и a3. Результирующая функция определяется по следующей формуле (τ = 1):

2. Вычислить аналитически определенный интеграл  .
.
3. Разработать программу, вычисляющую величину F методом Монте-Карло при заданном числе экспериментов.
4. При помощи разработанной программы вычислить определенный интеграл  при N = 2i экспериментах, где
при N = 2i экспериментах, где 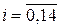 .
.
4. Варианты заданий
Таблица 1. Варианты заданий к лабораторной работе №1
| № варианта | a1 | f1(t) | a2 | f2(t) | a3 | f3(t) |
| -1 | -1 | |||||
| 4,5 | -4,5 | |||||
| -5 | -2,5 | |||||
| 1,5 | ||||||
| -1 | ||||||
| 2,5 | ||||||
| 2,5 | ||||||
| -10 | -30 | |||||
| -7 | -21 | |||||
| 3,5 | -3,5 | |||||
| -2 | -2 | |||||
| -5 | ||||||
| -9 | ||||||
| 2,5 | -2,5 | |||||
| -4 | -2 | |||||
| -8 | ||||||
| -5 | ||||||
| -27 | -27 | |||||
| -15 | ||||||
| 1,5 | -1,5 |
Перечень функций:
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
3. Содержание отчета
1. Цель работы.
2. График функции  .
.
3. Аналитический расчет величины F.
4. Описание разработанной программы: список использованных переменных, блок-схема, текст программы.
5. Табличное представление результатов моделирования  .
.
6. График по рассчитанной таблице. Ось абсцисс представить в логарифмическом масштабе по основанию 2. На графике отметить уровнем величину F.
7. Выводы.
4. Вопросы для самопроверки
1. Объясните два алгоритма оценки определенного интеграла методом Монте-Карло. Назовите преимущества и недостатки каждого.
2. Вычислите математическое ожидание оценки площади методом Монте-Карло.
3. Обоснуйте гипотезу о нормальном распределении вероятностей для оценки определенного интеграла по методу Монте-Карло.
4. Какие величины связываются неравенством Чебышева.
5. Сформулируйте теорему Бернулли.
6. Сформулируйте закон трёх сигма.
7. Как зависит погрешность оценки площади от числа экспериментов?
5. Список рекомендованной литературы
1. Вентцель Е. С. Теория вероятности. М.: Наука. 1969 г.
2. Соболь И. М. Метод Монте-Карло. М.: Наука. 1985 г.
3. Бусленко Н. П., Голенко Д. И., Соболь И. М., Срагович В. Г., Шрейдер Ю. А. Метод статистических испытаний (метод Монте-Карло). М.: Физматгиз. 1962 г.
Лабораторная работа №2
Датчики случайных чисел. Построение гистограмм.
1. Необходимые теоретические сведения.
Введение
При имитационном моделировании разработчику модели часто требуется формировать на ЭВМ последовательности случайных чисел, отображающие реальный случайный процесс. Одной из основных характеристик случайного процесса является его закон распределения вероятностей, и погрешность моделирования определяется, прежде всего, тем, насколько точно воспроизводится закон распределения вероятностей случайной величины.
Таким образом, необходима методика построения датчиков случайных чисел с заданным законом распределения вероятностей, а также методика оценки точности работы датчика.
В последующем изложении закон и плотность распределения вероятностей считаются синонимами. При этом, слово «вероятностей» в отдельных случаях для сокращения текста может быть опущено.
Дата добавления: 2015-02-10; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |