Основные характеристики ЭСМО

Для оценки эффективности работы СМО используется ряд характеристик. При этом интересы владельца СМО и ее пользователя могут не совпадать. В частности, для владельца важны такие характеристики как производительность системы и ее стоимость, в то время как для пользователя представляют интерес оперативность системы и вероятность отказа в обслуживании.

Производительность системы Q равна среднему числу запросов, обслуживаемых системой в единицу времени. Производительность СМО не может быть больше интенсивности входного потока запросов l, так как не может быть обслужено больше запросов, чем их поступило в СМО. Кроме того, производительность СМО не превосходит интенсивности обслуживания m, так как в предельном случае, когда сервер работает без простоев, его производительность m как раз и определяет производительность СМО. Таким образом, верна оценка

С точки зрения эксплуатации системы важной характеристикой является коэффициент загрузки системы

который показывает, насколько эффективно используется система, т.е. какую долю времени система действительно обрабатывает запросы, а не простаивает.

Для системы с бесконечным буфером все заявки поступают в буфер и в конечном итоге обслуживаются, поэтому вероятность отказа в обслуживании для такой системы равна нулю.

Оперативность СМО (т. е. время ее реакции на запрос) обычно характеризуют средним значением времени пребывания запроса в системе. Это время T складывается в общем случае из времени ожидания запроса в буфере и времени обработки запроса в сервере. Среднее время пребывания запроса в системе связано со средним числом запросов в системе L_сист простой формулой, известной как теорема Литтла:

Если входной поток запросов является пуассоновским, то для вычисления Tможно воспользоваться формулой Поллачека–Хинчина:

Стоимость ЭСМО в простейшем случае представляется в виде суммы стоимостей буфера и сервера, причем, стоимость буфера считается линейной функцией от объема буфера N,а стоимость сервера считается линейной функцией от его производительности m. Тогда формула для стоимости СМО имеет вид:

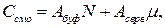
где A_буф и A_серв - некоторые коэффициенты. Отметим, что на практике зависимость C_смо от аргументов может быть более сложной, но в любом случае она должна оставаться монотонно не убывающей от величин mи N.