Рекомендации по моделированию СМО

Для увеличения скорости моделирования СМО целесообразно использовать, подход, называющийся «моделированием по событиям». Основные принципы этого подхода были изложены во вводной части к третьей лабораторной работе. Итак, в ЭСМО присутствуют следующие особые события: поступление заявки в СМО, прием заявки на обслуживание, окончание обслуживания заявки.

Тогда состояние СМО будет описываться следующим набором переменных:

1. t_с - системное время.

2. zan – переменная, равная единице, если ОУ занят, и нулю, если ОУ свободен.

3. t_з - следующий момент поступления заявки.

4. t_осв - следующий момент освобождения ОУ.

5. n – количество заявок, поступивших к данному моменту в СМО.

6. k – количество заявок, обслуженных к данному моменту в ОУ.

7. m – количество заявок в буфере.

Программа должна заданное число раз выполнить следующий перечень действий: определение момента следующего особого события, имитация события, корректировка результатов. Обобщенный алгоритм исследования различных параметров СМО представлен на рис. 5.

Существует ряд подходов к выбору условия окончания моделирования. Один из них заключается в построении гистограмм распределения входного потока заявок и времени обслуживания. Как только для гистограмм этих распределений выполнятся условия, приведенные в лабораторной работе №2, моделирование можно считать выполненным. Можно так же воспользоваться правилом, предложенным в лабораторной работе №3.

Для оценки правильности составленной модели необходимо провести тестовое испытание при пуассоновском входном потоке. Полученный результат T(l,m₀) можно проверить при помощи формулы Поллачека-Хинчина.

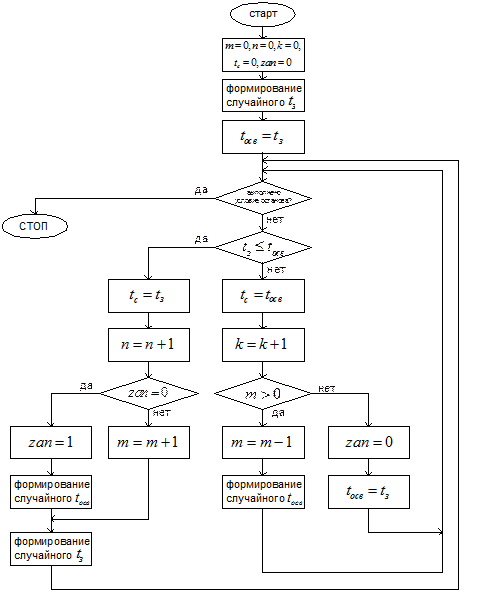
Рис. 5. Алгоритм исследования характеристик ЭСМО