КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цель работы
Нахождение экспериментальной зависимости T(l,m0) для элементарной системы массового обслуживания с бесконечным буфером.
Порядок выполнения работы
1. Выбрать вариант задания из таблицы 6.
2. В соответствии с вариантом составить и отладить моделирующую программу.
3. Провести моделирование для тестового примера. Отладить программу на тестовом примере. Подобрать объем моделирования Nтак, чтобы относительная погрешность экспериментальных данных для тестового примера не превосходила 10%;
4. Провести моделирование для получения требуемой экспериментальной зависимости при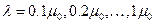 
. Полученные данные внести в таблицу 5.
Таблица 5 – Зависимость среднего времени пребывания запроса от интенсивности входного потока
| l | 0.1m0 | 0.2m0 | 0.3m0 | 0.4m0 | 0.5m0 | 0.6m0 | 0.7m0 | 0.8m0 | 0.9m0 | 1m0 |
| T |
Варианты заданий
Таблица 6 – Варианты заданий к лабораторной работе №4
| № варианта | Закон распределения входного потока заявок fзаявок(x) | Закон распределения времени обслуживания заявок fобслуж(x) | m0 |
| Равномерный | Эрланговский 2 порядка | ||
| Равномерный | Эрланговский 3 порядка | ||
| Равномерный | Эрланговский 4 порядка | ||
| Равномерный | Эрланговский 5 порядка | ||
| Равномерный | Эрланговский 6 порядка | ||
| Эрланговский 2 порядка | равномерный | ||
| Эрланговский 3 порядка | равномерный | ||
| Эрланговский 4 порядка | равномерный | ||
| Эрланговский 5 порядка | равномерный | ||
| Эрланговский 6 порядка | равномерный | ||
| Равномерный | Экспоненциальный | ||
| Равномерный | Экспоненциальный | ||
| Равномерный | Экспоненциальный | ||
| Равномерный | Экспоненциальный | ||
| Равномерный | Экспоненциальный | ||
| Экспоненциальный | равномерный | ||
| Экспоненциальный | Равномерный | ||
| Экспоненциальный | Равномерный | ||
| Экспоненциальный | Равномерный | ||
| Экспоненциальный | Равномерный | ||
| Эрланговский 2 порядка | Экспоненциальный | ||
| Эрланговский 3 порядка | Экспоненциальный | ||
| Эрланговский 4 порядка | Экспоненциальный | ||
| Эрланговский 5 порядка | Экспоненциальный | ||
| Эрланговский 6 порядка | Экспоненциальный |
Для равномерного закона распределения вероятностей границы интервала значений случайной величины выбрать так, чтобы длина интервала равнялась 0.1m0.
Содержание отчета
1. Цель работы.
2. Формулы и графики законов распределения вероятностей для интервалов между заявками и времени обслуживания заявок.
5. Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.
6. Теоретический и экспериментальный графики зависимости среднего времени пребывания заявки в системе от интенсивности входного потока для тестового примера.
7. Данные таблицы 5 и построенный по ним график.
8. Выводы.
Вопросы для самопроверки
1. Назовите основные элементы СМО и их характеристики.
2. Как оценивается КПД для системы массового обслуживания?
3. Как связаны средняя длина очереди и среднее время пребывания заявки в очереди?
4. Как связаны средняя длина очереди и среднее число заявок в СМО?
5. Как связаны среднее время пребывания заявок в СМО и среднее число заявок в СМО?
6. Приведите формулу для среднего времени пребывания заявки в системе, когда входной поток заявок – пуассоновский, а поток обслуживания – рекуррентный.
7. Список рекомендованной литературы
1. Вентцель Е. С. Теория вероятности. М.: Наука. 1969 г.
2. Строгалев В. П., Толкачева И. О., Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.
3. Плакс Б. И. Имитационное моделирование систем массового обслуживания. СПб.: Издательство СПбГААП, 1995.
Дата добавления: 2015-02-10; просмотров: 189; Мы поможем в написании вашей работы!; Нарушение авторских прав |